概要
温度の異なる物体表面と流体との間には対流伝熱が生じます。このときの伝熱量と温度差の関係式をニュートンの冷却法則といいます。
$$q=h(T_{w}-T_{bulk})・・・(1)$$
q:熱流束[W/m2]、h:境膜伝熱係数[W/(m2・K)]
Tw:壁面温度[K]、Tbulk:流体のバルク温度[K]
ニュートンの冷却法則は(1)式で表されます。
式の形は伝導伝熱を表わすフーリエの法則と似ていますが、大きく異なる点は比例定数です。
フーリエの法則の比例定数である熱伝導度は物質固有の値であるのに対して、ニュートンの冷却法則の比例定数である境膜伝熱係数は流体の流れの状態により変化します。
したがって、境膜伝熱係数は算出するのが難しい比例定数となります。
ただし、プラントでよく見かける流体の流れはある程度パターンがあり、そのような系では境膜伝熱係数を算出するための実験式や半経験式があることが多いです。
加えて、対流伝熱は工業的にも主要な伝熱形態となりますので計算する機会も多いでしょう。
様々な境膜伝熱係数の算出方法
実務でよく計算する境膜伝熱係数の計算式や算出方法をまとめました。
熱交換器
管内(チューブ)側境膜伝熱係数
最もよく使用する式です。熱交換器だけでなく配管流れにも適用できます。
-

熱交換器【管内側境膜伝熱係数】を解説:チューブ内流れの伝熱
この記事では配管や熱交換器の伝熱管内を流れる流体の境膜伝熱係数についてまとめています。配管内の流動は他の流れに比べると単純で、種々の相関式が発表されています。
続きを見る
シェル側境膜伝熱係数
バッフルがある場合とない場合で使用する式が違います。
-

熱交換器【シェル側境膜伝熱係数】を解説:各計算式を比較
この記事では熱交換器のシェル側を流れる流体の境膜伝熱係数についてまとめています。配管内の流動と比べるとやや複雑な流れになりますが、種々のパラメータで補正をかけることでうまく相関できる式がいくつか発表されています。
続きを見る
撹拌槽
槽内側境膜伝熱係数
撹拌翼の種類ごとに境膜伝熱係数を求める式が違います。
-

撹拌槽【槽内側境膜伝熱係数(ジャケット伝熱)】を撹拌翼の種類ごとに解説
撹拌槽内の流動は撹拌翼のフローパターンによって変化するため、槽壁の境膜伝熱係数もそれに応じて変化します。先人達は境膜伝熱係数を比較的簡単な相関式で求められるよう研究してきました。以下ではその相関式について紹介します。
続きを見る
攪拌槽伝熱全般
槽内側境膜伝熱係数、ジャケット側境膜伝熱係数、あるいはコイルを使用する場合の境膜伝熱係数など、撹拌槽伝熱全般の計算式と伝熱の改善方法について記載しています。
-

【撹拌槽伝熱】総括伝熱係数U・伝熱面積A・温度差ΔTそれぞれの改善手法を徹底解説
この記事では撹拌槽の伝熱能力についての考え方や計算方法、どのようにすれば伝熱性能を改善させることができるのか、について解説しています。
続きを見る
熱流体解析ソフト(CFD)での取り扱い
熱流体解析ソフト(CFD)は近年かなり便利になっており、様々な値を出力することができます。
弊社で使用しているANSYS Fluentでは対流伝熱計算をした際には、壁熱伝達率[W/(m2・K)]というパラメータを出力することができます。
うまく利用すれば境膜伝熱係数を簡単に出力できる一方で、メッシュの切り方や設定を間違えると境膜伝熱係数とは異なる値が出力されてしまいます。
ここでは壁熱伝達率の扱いについて解説します。
(ソフトのバージョンによって壁熱伝達率の定義や計算方法が異なる可能性があることをご容赦願います。)
境膜伝熱係数の定義
通常のニュートンの粘性法則の定義です。
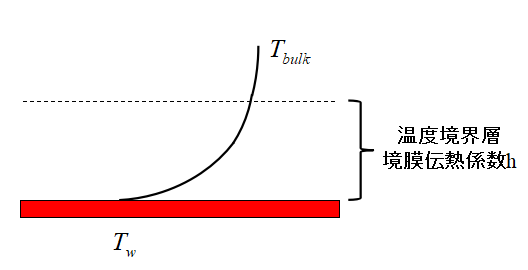
上図に壁面近傍の温度境界層を示します。
境膜伝熱係数は壁面温度と流体のバルク温度の差で定義され、(1)式のように表されます。
$$q=h(T_{w}-T_{bulk})・・・(1)$$
壁熱伝達率の定義
一方で、熱流体解析ソフト(Fluent)で出力できる壁熱伝達率の定義は(1)式とは異なります。
壁熱伝達率は壁面温度と壁面第一層のメッシュにおける温度の差で定義され(2)式のように表されます。
$$q=h(T_{w}-T_{f1})・・・(2)$$
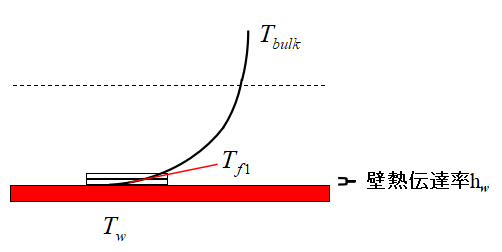
Fluentではメッシュのセル中心で値を計算しますから、壁面から第一層メッシュのセル中心までの温度差が取られます。
したがって、第一層のメッシュを細かくし過ぎると粘性底層の温度を拾ってしまい、壁熱伝達率の値は(1)式で定義される境膜伝熱係数とは異なる値となります。
これを回避する手段として、乱流域(バルク領域)にセル中心がくるようメッシュを切ることが挙げられます。
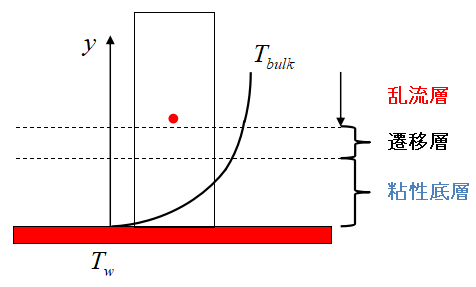
上図のようにメッシュを配置すれば境膜伝熱係数とほとんど同じ値となる壁熱伝達率が得られるでしょう。
このようなメッシュの切り方は、乱流場の解析で壁関数を使用する場合の一般的な手法であり、特別なことをしているわけではありません。
しかし最近はコンピュータの計算スペック向上に伴い、壁関数を使用せず壁面近傍のメッシュを細かく切るタイプの乱流モデルを使うことも増えています。
そのような場合には上記の理由から、壁熱伝達率が境膜伝熱係数と全く異なる値が得られてしまうため気をつける必要があります。
CFDをうまく使用することで、境膜伝熱係数を算出する実験式が適用できないような複雑な流れであっても、形状を再現して解析すれば境膜伝熱係数を得ることができ、装置設計の指針となります。



