概要
ラグランジュ(Lagrange)補間はあるデータを多項式で補間する手法の1つです。
補間法の中でも基礎的な位置付けにあり、初心者はまずこの手法から勉強するのが良いでしょう。
ただし実用上は後述するルンゲ(Runge)現象が生じ補間値が不安定になる可能性があるため、他の補完法を使用した方が良い場合もあります。
ラグランジュ補間式
(x1,y1)、(x2,y2)・・・(xn,yn)というようなn個のデータを多項式で表すことを考えます。
これらn個の点を通る式は
$$\begin{align}y&=a_{1}(x-x_{2})(x-x_{3})・・・(x-x_{n})+a_{2}(x-x_{1})(x-x_{3})・・・(x-x_{n})\\&+・・・+a_{n}(x-x_{1})(x-x_{2})・・・(x-x_{n-1})・・・(1)\end{align}$$
(1)式のような多項式で表されます。
この(1)式に例えば(x1,y1)を代入すれば係数a1が求められ、(x2,y2)を代入すれば係数a2が求められます。
この方法で係数a1a2・・・anまで算出し、(1)式に代入して整理すると最終的に
$$\begin{align}y&=y_{1}\frac{(x-x_{2})(x-x_{3})・・・(x-x_{n})}{(x_{1}-x_{2})(x_{1}-x_{3})・・・(x_{1}-x_{n})}+ y_{2}\frac{(x-x_{1})(x-x_{3})・・・(x-x_{n})}{(x_{2}-x_{1})(x_{2}-x_{3})・・・(x_{2}-x_{n})}+\\&・・・+y_{n}\frac{(x-x_{1})(x-x_{2})・・・(x-x_{n-1})}{(x_{n}-x_{1})(x_{n}-x_{2})・・・(x_{n}-x_{n-1})}・・・(2)\end{align}$$
(2)式が得られます。この(2)式を使用してデータを補間する手法をラグランジュ補間といいます。
Excel計算例
計算条件
(2)式の一般式ではピンとこないと思いますので実際にExcelで計算してみましょう。
$$(x_{1},y_{1})=(0.10,3.5)$$
$$(x_{2},y_{2})=(0.15,3.0)$$
$$(x_{3},y_{3})=(0.20,2.8)$$
$$(x_{4},y_{4})=(0.25,2.5)$$
上で示すような4点のデータをラグランジュ補間します。
データの数はいくつあっても補間できますが、Excelで手打ちで入力することを考えると4点でもかなり面倒くさいです。
データの数が多い場合にはマクロを組むかPython等のプログラミング言語を利用するのが良いでしょう。
今回は頑張ってExcelでやっています。
計算設定
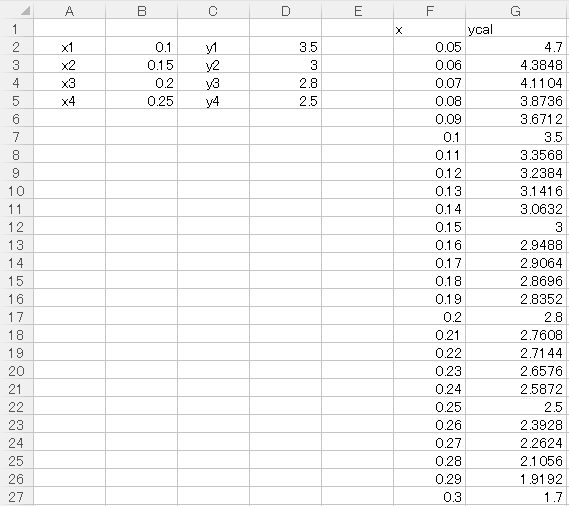
上図にExcelでの計算シートを示しています。
B2~B5セルにx1~x4、D2~D5セルにy1~y4を入力しています。
Fの列には任意のxを入力しています。xの範囲はなんでもよいのですが、適度に外挿も含めてx=0.05~0.3まで0.01刻みで設定しました。
あとはメインの(2)式によるyの値の計算です。
とはいっても、(2)式をn=4の場合として考えて入力するだけです。
$$\begin{align}y&=y_{1}\frac{(x-x_{2})(x-x_{3})(x-x_{4})}{(x_{1}-x_{2})(x_{1}-x_{3})(x_{1}-x_{4})}+ y_{2}\frac{(x-x_{1})(x-x_{3})(x-x_{4})}{(x_{2}-x_{1})(x_{2}-x_{3})(x_{2}-x_{4})}\\&+y_{3}\frac{(x-x_{1})(x-x_{2})(x-x_{4})}{(x_{3}-x_{1})(x_{3}-x_{2})(x_{3}-x_{4})}+y_{4}\frac{(x-x_{1})(x-x_{2})(x-x_{3})}{(x_{4}-x_{1})(x_{4}-x_{2})(x_{4}-x_{3})}・・・(3)\end{align}$$
n=4と考えると(3)式のようになります。
あとはGの列にycalとして(3)式を入力していきます。任意の値xは固定せず、他のx1~x4、y1~y4を$で固定しておけばコピペするのが楽になるでしょう。
それでもかなり面倒くさいですが。
計算結果
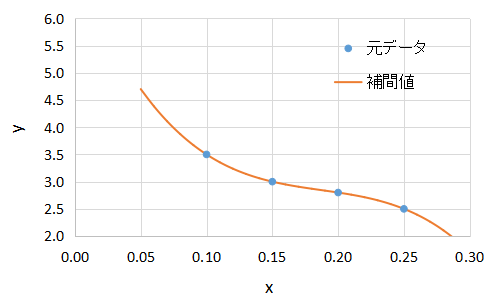
上図に計算結果をグラフにしたものを示します。
元データを滑らかに繋いで補間する曲線が引けていますね。外挿部分もそれっぽく補間していますが、どの程度の妥当性があるのかは元データの理論的背景から判断するしかないと思います。
ルンゲ現象
データの点数が増えていき、補間多項式が高次になるとグラフの形状が不安定になる現象が起こることがあります。
これはルンゲ現象と呼ばれています。

上図にルンゲ現象が確認された例を示しています。
元データのプロットからするとほぼ直線に近いような補間が望ましいのですが、x=12~20の区間でyの値が大きく変化して不安定な補間となっています。
元データのプロットの数を変更してもなかなか改善されないケースがあるので悩ましいところです。
そのためルンゲ現象が確認された場合は他の補間法を使用するのが手っ取り早い解決策となるでしょう。
まとめ
補間手法の基礎であるラグランジュ補間法について解説しました。
最近は機械学習等でこのようなデータの加工をする機会があるかもしれませんので覚えておきましょう。
