概要
粒子が小さくなると慣性力が働きにくくなり、粒子は流体と同じ運動をするようになります。
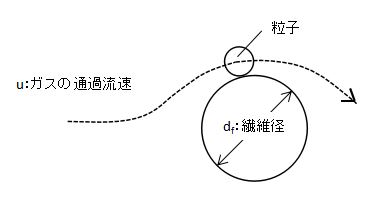
ですが、流体分子と比較すると粒子は圧倒的に大きいです。
そのため障害物近傍を通過するとき、ガス分子は通過できますが、粒子は障害物に物理的にさえぎられて捕集されます。
この捕集機構をさえぎり捕集機構といいます。
さえぎり捕集機構は捕集効率が高い領域が慣性捕集機構と被るため、さえぎり捕集単独で捕集するような装置設計は難しいでしょう。
単一繊維捕集効率を求める際は、慣性捕集効率とさえぎり捕集効率はセットで考える必要があります。
捕集効率推算
さえぎりパラメータ
さえぎり捕集効率を推算するうえで重要なのが、さえぎりパラメータR[-]です。
$$R=\frac{d_{p}}{d_{f}}・・・(1)$$
dp:粒子径[m]、df:繊維径[m]
(1)式のように粒子径と繊維径の比で表されます。
繊維径に対して粒子径が大きくなるほどさえぎられやすくなり、捕集効率が増加します。
推算式
ここでは、さえぎり捕集効率ηR[-]のいくつか有名な推算式を紹介します。
Langmuirの式
$$η_{R}=\frac{2(1+R){\rm{ln}}(1+R)-(1+R)+1/(1+R)}{2(2-{\rm{ln}}Re_{f})}・・・(2)$$
$$Re_{f}=\frac{ρud_{f}}{μ}・・・(3)$$
Ref:繊維レイノルズ数[-]、ρ:流体密度[kg/m3]
u:流速[m/s]、μ:流体粘度[Pa・s]
比較的古い式として、Langmuirの式があります。繊維レイノルズ数Ref<1で成り立つとされています。
この式の特徴として、さえぎり捕集効率ηRが繊維レイノルズ数Ref中の流速uに依存する点が挙げられます。
というのも、さえぎり捕集効率の推算式は流速uに依存しないものが多いためです。
また、さえぎり捕集効率をさえぎりパラメータRに対してプロットしたものを以下に示します。
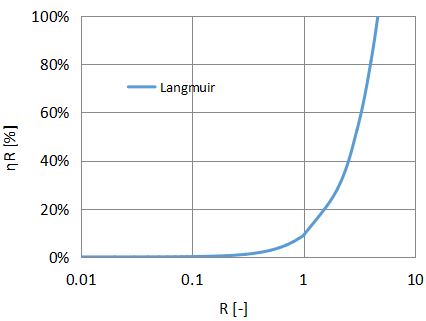
u=0.01m/s、Ref=0.01
R=1より大きくなる、つまり繊維径dfより粒子径dpが大きくなると急激に捕集効率が増加することがわかります。
Kirsch and Stechkinaの式
$$η_{R}=\frac{1+R}{2Ku}[2{\rm{ln}}(1+R)-1+α+(\frac{1}{1+R})^{2}(1-\frac{α}{2})-\frac{α}{2}(1+R)^2]・・・(4)$$
$$Ku=-0.5{\rm{ln}}α+α-0.25α^2-0.75・・・(5)$$
Ku:水力学因子[-]、α:繊維の充填率[-]
その他古くからある有名な式として、KirschとStechkinaが発表した(4)式があります。
Kuは水力学因子で、桑原が発表した(5)式が採用されています。
同様に、さえぎり捕集効率をさえぎりパラメータRに対してプロットしたものを以下に示します。
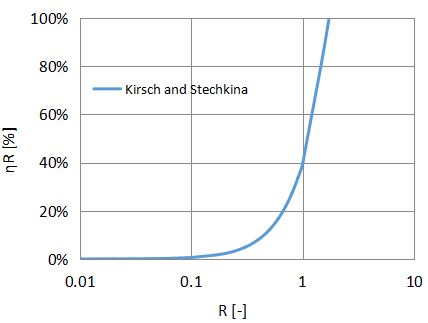
α=0.01、Ku=1.56
Langmuirの式よりもさえぎり捕集効率が
Liu and Rubowの式
$$η_{R}=0.6\frac{1-α}{Ku}\frac{R^2}{1+R}(1+\frac{1.996Kn_{f}}{R})・・・(6)$$
$$Kn_{f}=\frac{2λ}{d_{f}}・・・(7)$$
Knf:繊維クヌッセン数[-]、λ:ガス分子の平均自由行程[-]、df:繊維径[m]
クヌッセン数が小さい場合のガススリップを考慮してさえぎり捕集効率を推算する式を、LiuとRubowが発表しました。
同様に、さえぎり捕集効率をさえぎりパラメータRに対してプロットしたものを以下に示します。

α=0.01、Ku=1.56、df=10μm、Knf=0.013
繊維径dfが小さく、繊維クヌッセン数Knfが大きい場合にはガススリップの影響を無視できないため、(6)式を使用するのがよいでしょう。
まとめ
さえぎり捕集機構について解説しました。
捕集する粒子径が繊維径と同程度以上の大きさであれば、さえぎり捕集効果を考慮すべきだと思います。
