概要
Direct法は非線形方程式を解く手法の1つです。
逐次代入法とも呼ばれており、初期値xから得られたyの値をそのまま次のステップのxの値に代入して計算する手法です。
非線形方程式の解法の中では基本的な計算手法です。Direct法をベースにして修正された計算モデルも存在するので、まずはこの手法を勉強しておきましょう。
原理
方程式f(x)=0の解を求めることを考えます。
Direct法ではf(x)=0を変形して、
$$x=g(x)・・・(1)$$
(1)式のような形で計算します。
初期値x0からg(x0)が求まり、(1)式から次のx1を求めることができます。図で書くと、
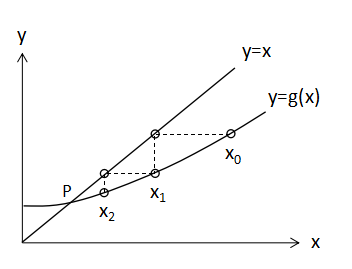
上のように繰り返し計算を実施し、最終的にy=g(x)とy=xとの交点Pを求めることでf(x)=0の解を算出することができます。
ただし、Direct法では
$$|g'(x)|>1・・・(2)$$
だと発散することが知られています。y=g(x)とy=xの位置関係が重要で、図で書くと、
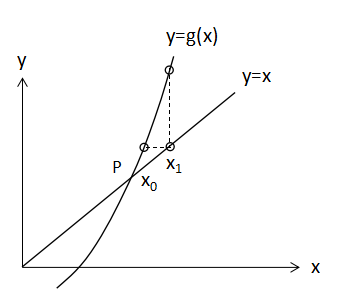
上のようになると繰り返し計算をすることで交点Pから離れていくので発散します。このようになる条件が(2)式です。
ちなみに、このような発散を回避できる計算モデルであるWegstein法が後に発表されています。
表計算ソフト計算例
実際にDirect法を使って表計算ソフトで計算してみましょう。
ここでは、
$$f(x)=1+\frac{1}{x}-x=0・・・(3)$$
(3)式についてDirect法で計算してみます。
(3)式に辺々xを足すと、
$$x=1+\frac{1}{x}$$
となります。したがって、
$$g(x)=1+\frac{1}{x}・・・(4)$$
(4)式とy=xとの交点をDirect法の繰り返し計算で求めていくことになります。
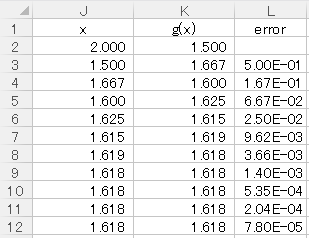
上に表計算ソフトでの計算を示しています。
まず適当に初期値を決定し、J2セルに入力します。ここではx0=2としています。
次にK2セルに(4)式を入力します。
次にJ3セルに、
$$J3セル=K2セル$$
と入力し、Direct法でxの値を更新します。
続いてerror値をL3セルに設定します。今回は
$$|J_{n+1}セル-J_{n}セル|<10^{-4}$$
となれば収束したとみなします。
後は収束するまで下にセルをコピーしていくだけです。結果として、x12=1.618のときにerror値<10-4となり収束しました。
また、この計算例におけるDirect法の収束計算のイメージを下のグラフに示します。
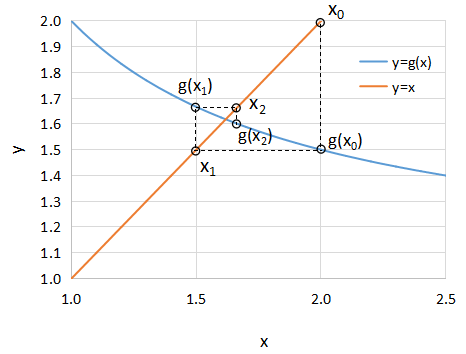
このように繰り返し計算が進むにつれて、y=g(x)とy=xの交点に近くなり収束していっています。
まとめ
非線形方程式を解く手法の1つであるDirect法について解説しました。
関数g(x)の値を次のステップのxの値として使用する計算手法です。計算する関数次第で収束しないこともあるので注意しましょう。
