概要
粒子が非常に小さくなると、ランダムな軌道で運動するようになります。

これをブラウン運動といい、この運動により粒子を捕集する機構を拡散捕集機構といいます。
拡散捕集は小さな粒子を捕集する場合の支配的な機構です。
流体の条件にもよりますが、0.1μm以下の大きさの粒子を捕集するときに考慮することが多いです。
捕集効率推算
ぺクレ数
拡散捕集を考えるうえで重要なパラメータがぺクレ数です。
$$Pe=\frac{ud_{f}}{D}・・・(1)$$
$$D=\frac{k_{B}TC_{c}}{3πμd_{p}}・・・(2)$$
u:面速度[m/s]、df:繊維径[m]、D:粒子の拡散係数[m2/s]
kB:ボルツマン定数[m2kg/(s2K)]、T:絶対温度[K]、Cc:カニンガムの補正係数[-]
μ:粘度[Pa・s]、dp:粒子径[m]
ぺクレ数が小さいほど拡散効果が大きくなり、捕集されやすくなります。
推算式
ここでは、拡散捕集効率ηD[-]のいくつか有名な推算式を紹介します。
Wang et al.
$$η_{D}=0.84Pe^{-0.43}・・・(3)$$
比較的簡単なものとして、Wangらの発表した(3)式があります。
(3)式は拡散係数が大きく、ぺクレ数Peが小さい領域を対象にしています。
また、拡散捕集効率をぺクレ数Peに対してプロットしたものを以下に示します。
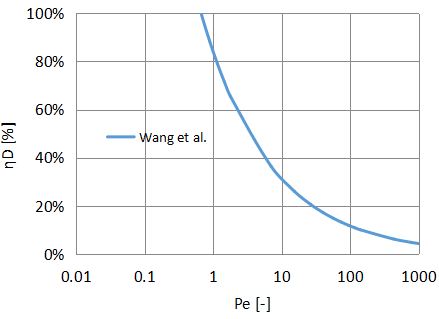
u=0.01m/s、df=10μm
Pe<10の領域において、高い拡散捕集効率を示すことがわかります。
Stechkina et al.
$$η_{D}=2.9Ku^{-1/3}Pe^{-2/3}+0.62Pe^{-1}・・・(4)$$
$$Ku=-0.5{\rm{ln}}α+α-0.25α^2-0.75・・・(5)$$
Ku:水力学因子[-]、α:繊維の充填率[-]
Wangらの式は簡単でよいですが、ガス-繊維界面での流れ場の歪みの影響を含んでいません。
そこでStechkinaらは桑原の水力学因子を使用して、(4)式を発表しました。
水力学因子は、粒子が繊維に近接することで発生する流れ場の歪みを補正するパラメータです。
同様に、拡散捕集効率をぺクレ数Peに対してプロットしたものを以下に示します。
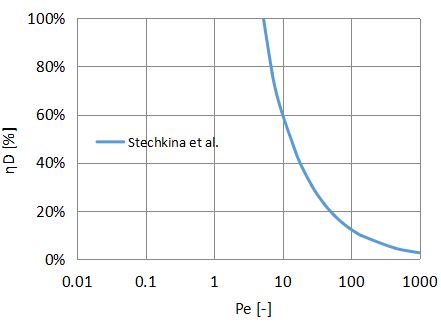
u=0.01m/s、
Pe<100の領域において、高い拡散捕集効率を示すことがわかります。
Payet et al.
$$η_{D}=1.6(\frac{1-α}{Ku})^{1/3}Pe^{-2/3}C_{1}C_{2}・・・(6)$$
$$C_{1}=1+0.388Kn_{f}[(1-α)\frac{Pe}{Ku}]^{1/3}・・・(7)$$
$$C_{2}=\frac{1}{1+1.6(\frac{1-α}{Ku})^{1/3}Pe^{-2/3}C_{1}}・・・(8)$$
繊維径が非常に小さくなり、ガス分子の平均自由行程に近い値となるとガス分子が繊維表面で滑るようになります。
Payetらはこのスリップ流れを考慮した(6)式を発表しました。
同様に、拡散捕集効率をぺクレ数Peに対してプロットしたものを以下に示します。
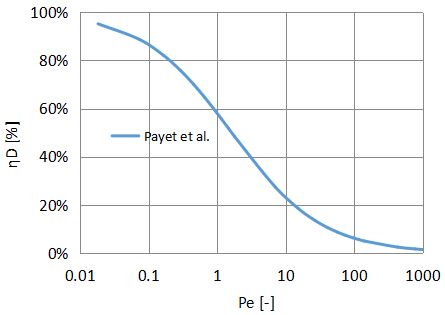
ぺクレ数が小さくなると捕集効率が100%を超える推算式が多いのですが、Payetらのモデルは100%を超えないように補正項が加えられています。
まとめ
拡散捕集機構について解説しました。
繊維充填層式のフィルターを使用する場合は拡散捕集を考慮して捕集効率を推算しましょう。
