【カニンガムの補正係数】について解説：粒子が受ける抵抗力の補正

概要

気体中を運動する粒子が受ける抵抗力はStokesの式で計算することができ、気体が連続流体とみなせる場合は実現象とよく一致します。

一方で粒子が微細になる、あるいは圧力が低くなると気体分子の不連続性が影響するようになり、粒子表面でガス分子がすべるため粒子への抵抗力が弱まります。

このような粒子が微細な場合でもStokesの式で計算できるように補正する係数をカニンガム(Cunningham)の補正係数といいます。

学問的にはエアロゾルを扱う分野では重要な補正となっています。

また、実プラントにおいては微粒子の集塵・捕集において考慮すべき補正係数だと言えます。

クヌッセン数K_n

気体分子の不連続性が影響するかどうかはクヌッセン数K_nで判定できます。

$$K_{n}=\frac{2λ}{d_{p}}・・・(1)$$

λ：気体分子の平均自由行程[m]、d_p：粒子径[m]

K_n<<0.01であれば気体は連続流体として扱うことができます。

逆にK_n>>10だと気体分子の不連続性の影響があるため、Stokesの式で抵抗力を計算する際には補正が必須となります。

カニンガムの補正係数C_c

一般形

カニンガムの補正係数C_cは、一般にクヌッセン数K_nを使用して、

$$C_{C}=1+K_{me}K_{n}・・・(2)$$

$$K_{me}=A+B・{\rm{exp}}(-C/K_{n})・・・(3)$$

A、B、C：定数[-]

(2)、(3)式で表されます。

A、B、Cの定数は参考文献によって様々な値が与えられています。

ここでは例としてDaviesの値を参考にすると、

• A=1.257
• B=0.400
• C=1.100

となります。

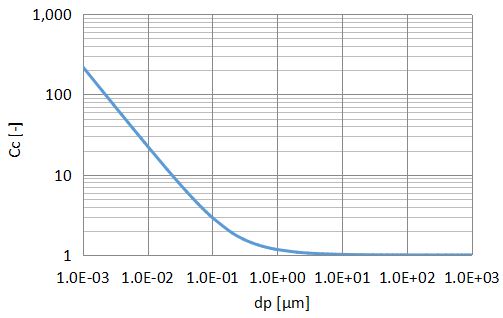
例として、平均自由行程λ=67nmのときのクヌッセン数K_n及び粒子径d_pとカニンガムの補正係数C_cの関係を下図に示します。

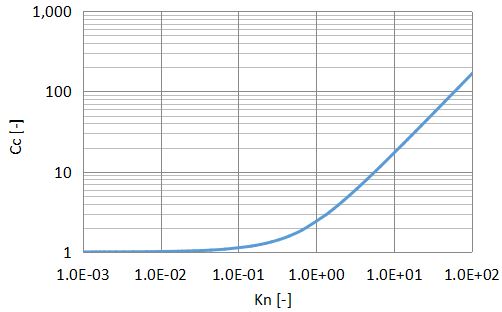
K_nが0.01以下のときはCc≒1となっており、カニンガムの補正係数C_cが必要ないことがわかります。

逆にK_nが1.0以上のときはCcが2.0以上の値を取っており、補正が必要であることがわかります。

また、粒子径では10μm以上となるとCc≒1となり、カニンガムの補正係数C_cが必要ないことがわかります。

1つの目安として覚えておくとよいです。

圧力考慮

系の圧力が低くなると分子の数が少なくなるため、同様に気体分子の不連続性が確認されます。

Hindsは圧力変化による影響を加味したカニンガムの補正係数C_cを(4)式としました。

$$C_{c}=1+(\frac{2}{Pd_{p}}){6.32+2.01\rm{exp}}(-0.1095Pd_{p})・・・(4)$$

P：絶対圧力[cmHg]、d_p：粒子径[μm]

Pやd_pは単位に気を付けましょう。

例として、平均自由行程λ=67nmのときの圧力変化の影響を下図に示します。

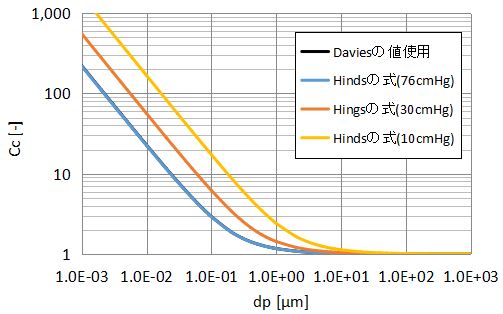
76cmHgで大気圧のときはDaviesの値を使用した場合と一致しました。

30cmHg、10cmHgと圧力を低くするにつれC_cの値が大きくなったため、不連続性の影響が大きくなり、補正も大きくする必要があることがわかります。

平均自由行程λ

カニンガムの補正係数C_cの算出のために(2)、(3)式を使用するためには平均自由行程λを算出する必要があります。

温度T[K]、圧力P[mmHg]での空気中における平均自由行程λ[μm]は、

$$λ≒0.031\frac{T^{1.3}}{P}・・・(5)$$

(5)式で近似されます。

まとめ

カニンガム(Cunningham)の補正係数について解説しました。

微粒子を扱う場合は必要になる補正係数です。