概要
吸着剤表面に多分子として吸着すると仮定し導出された(1)式をBETの吸着等温式といいます。
$$q=\frac{q_{m}Cp}{(p_{0}-p)[1+(C-1)p/p_{0}]}・・・(1)$$
q:吸着量[kg/(kg-吸着剤)]、qm:飽和吸着量[kg/(kg-吸着剤)]
p:平衡分圧[-]、p0:飽和蒸気圧[-]、C:定数[-]
BETの吸着等温式は、吸着材の比表面積を算出するのによく使用されます。
本記事では、BETの吸着等温式の導出等について解説します。
BETの吸着等温式の導出
仮定
BETの吸着等温式の導出にあたっては、いくつかの仮定を置いています。
- 第1層以外の全ての吸着層での吸着熱は、吸着質のモル凝縮熱と等しい。
- 第1層以外での吸着・脱着の頻度因子は一定である。
- 飽和蒸気圧p0では、吸着質は固体表面上で凝縮し吸着層数は無限大となる。
導出
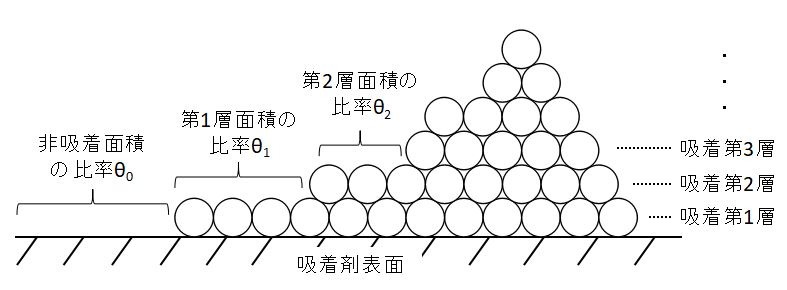
上図のような多分子吸着を考えます。
吸着剤表面のうち、吸着剤分子で覆われていない面積の比率をθ0とします。
次に第1層の吸着剤分子で覆われた面積の比率をθ1、第2層の吸着剤分子で覆われた面積の比率をθ2とし、第i層の吸着剤分子で覆われた面積の比率をθiとします。
このとき、各比率の間には、
$$θ_{0}=1-\sum_{i=1}^{∞} θ_{i}・・・(2)$$
(2)式が成り立ちます。
また、吸着分子1個の占有面積をσ[cm2]、表面1cm2当たりの吸着分子数をNa[1/cm2]とすると、吸着剤全表面積の吸着分子数Naσは、
$$N_{a}σ=θ_{1}+2θ_{2}+・・・+iθ_{i}+・・・=\sum_{i=1}^{∞}iθ_{i}・・・(3)$$
(3)式で表されます。
次に吸着平衡を考えます。
まず第1層目に注目すると、未吸着の面積(θ0)に分子が吸着する確率と、第1層(θ1)から分子が脱離する確率は等しいので、
$$Nθ_{0}=\frac{ν_{1}θ_{1}}{σ}・・・(4)$$
N:1秒間に1cm2の表面に飛来する分子数[1/(cm2・s)]
ν1:第1層分子が脱離する速度定数[s-1]
(4)式が成り立ちます。
同様に、第2層についても、
$$Nθ_{1}=\frac{ν_{2}θ_{2}}{σ}・・・(5)$$
(5)式が成り立ちます。したがって、一般化すると、
$$Nθ_{i-1}=\frac{ν_{i}θ_{i}}{σ}・・・(6)$$
(6)式となります。(4)~(6)式を式変形すると、
$$θ_{1}=\frac{σN}{ν_{1}}θ_{0}・・・(7)$$
$$θ_{2}=\frac{σN}{ν_{2}}θ_{1}・・・(8)$$
:
$$θ_{i}=\frac{σN}{ν_{i}}θ_{i-1}・・・(9)$$
(7)~(9)式となります。
ここで、第2層以上の吸着状態は同一である仮定から、
$$ν_{2}=ν_{3}=・・・=ν_{i}=・・・\ ・・・(10)$$
(10)式となります。また、
$$x=\frac{σN}{ν_{2}}・・(11)$$
(11)式とおいて簡略化します。
(7)~(11)式から、
$$θ_{1}=\frac{σN}{ν_{1}}θ_{0}=\frac{ν_{2}}{ν_{1}}xθ_{0}・・・(12)$$
$$θ_{2}=\frac{σN}{ν_{2}}θ_{1}=xθ_{1}=\frac{ν_{2}}{ν_{1}}x^{2}θ_{0}・・・(13)$$
$$θ_{3}=\frac{σN}{ν_{3}}θ_{2}=x^{2}θ_{1}=\frac{ν_{2}}{ν_{1}}x^{3}θ_{0}・・・(14)$$
:
$$θ_{i}=\frac{σN}{ν_{i}}θ_{i-1}=x^{i-1}θ_{1}=\frac{ν_{2}}{ν_{1}}x^{i}θ_{0}・・・(15)$$
一般化すると(15)式となります。
ここで、
$$C=\frac{ν_{2}}{ν_{1}}・・・(16)$$
(16)式とおきつつ、(15)式を(2)、(3)式に代入すると、
$$θ_{0}=1-\sum_{i=1}^{∞} θ_{i}=1-Cθ_{0}\sum_{i=1}^{∞} x^{i}・・・(17)$$
$$N_{a}σ=\sum_{i=1}^{∞}iθ_{i}=Cθ_{0}\sum_{i=1}^{∞}ix^{i}・・・(18)$$
(17)、(18)式となります。
次に(17)式をθ0=に変形して(18)式に代入すると、(19)式となります。
$$θ_{0}=\frac{1}{1+C\displaystyle\sum_{i=1}^{∞} x^{i}}$$
$$N_{a}σ=\frac{C\displaystyle\sum_{i=1}^{∞}ix^{i}}{1+C\displaystyle\sum_{i=1}^{∞} x^{i}}・・・(19)$$
ここで初項a1、公比rの等比数列anは、
$$\sum_{i=1}^{∞} a_{n}=\frac{a_{1}}{1-r}・・・(20)$$
(20)式となりますから、(17)式の和の部分に適用すると
$$\sum_{i=1}^{∞} x^{i}=\frac{x}{1-x}・・・(21)$$
(21)式となります。
また、(21)式をxで微分すると、
$$\sum_{i=1}^{∞} ix^{i-1}=\frac{1}{(1-x)^{2}}・・・(22)$$
(22)式となり、両辺にxをかけると
$$\sum_{i=1}^{∞} ix^{i}=\frac{x}{(1-x)^{2}}・・・(23)$$
(23)式となります。
(21)、(23)式を(19)式に代入すると、
$$N_{a}σ=\frac{C\frac{x}{(1-x)^{2}}}{1+C\frac{x}{1-x}}=\frac{Cx}{(1-x)[1+(C-1)x]}・・・(24)$$
(24)式となります。
ここで、(11)式で定義されたxの物理的意味を考えてみます。
ν2は吸着分子の脱離速度定数[s-1]を示し、σは吸着分子1個の占有面積[cm2]を示すため、ν2/σは1cm2の吸着剤表面から脱離していく分子数となります。
一方で、逆に吸着剤表面へ飛来するガス分子数をNsとすれば、吸着平衡において
$$N_{s}=\frac{ν_{2}}{σ}・・・(25)$$
(25)式が成立します。
したがって、(11)式は
$$x=\frac{σN}{ν_{2}}=\frac{N}{N_{s}}=\frac{P}{P_{0}}・・(26)$$
(26)式のように分圧Pと飽和蒸気圧P0の比で表すことができます。
次に(24)式の左辺について、吸着剤の表面積をA[cm2]、吸着量をq、飽和吸着量をqmとすると、
$$N_{a}σ=\frac{N_{a}A}{A/σ}=\frac{q}{q_{m}}・・・(27)$$
(27)式のように表すことができます。
(26)、(27)式を(24)式に代入し整理すると、
$$q=\frac{q_{m}Cp}{(p_{0}-p)[1+(C-1)p/p_{0}]}・・・(1)$$
冒頭の式の形となり、BETの吸着等温式が導出できました。
BETプロット
(1)の吸着等温線の定数を決定する場合、両辺逆数を取り変形すると、
$$\frac{p}{q(p_{0}-p)}=\frac{1}{q_{m}C}+\frac{C-1}{q_{m}C}\frac{P}{P_{0}}・・・(28)$$
(28)式となります。
縦軸p/[q(p0-p)]、横軸p/p0でプロットすることで、傾き(C-1)/(qmC)、切片1/(qmC)の直線が得られ、定数qm、Cを決定することができます。
おわりに
BETの吸着等温式を解説しました。
Langmuirの吸着等温式と並んで有名です。吸着剤の実験ではこの式を使用することも多いでしょう。
