概要
吸着剤表面に単分子として吸着すると仮定し導出された(1)式をLangmuirの吸着等温式といいます。
$$q=\frac{q_{∞}Kp}{1+Kp}・・・(1)$$
q:吸着量[kg/(kg-吸着剤)]、q∞:飽和吸着量[kg/(kg-吸着剤)]
p:平衡分圧[-]、K:吸着平衡定数[-]
Langmuirの吸着等温式は最も基礎的な等温式の1つであり、気相の吸着で系の圧力が低い場合に見られることが多いです。
本記事ではLangmuirの吸着等温式の導出等について解説します。
Langmuirの吸着等温式の導出
仮定
Langmuirの吸着等温式の導出にあたっては、いくつかの仮定を置いています。
- 吸着剤表面にはエネルギー的に均一な吸着サイトが存在する。
- 1つの気体分子が吸着サイトへ吸着されると、吸着は完了する。
- 吸着は可逆的で、脱離は吸着された分子の数に比例して発生する。
- 吸着した分子同士の相互作用はない。
特に2番目の仮定はLangmuirの吸着等温式が単分子層吸着と言われる所以となっています。
導出
気体分子が吸着しているサイトの割合をθとします。
まず吸着速度vaは、気体の分圧pと未吸着のサイトの割合1-θに比例すると考えると、
$$v_{a}=k_{a}p(1-θ)・・・(2)$$
(2)式のように表すことができます。
また脱着速度vdは、吸着サイトの割合θに比例すると考えると、
$$v_{d}=k_{d}θ・・・(3)$$
(3)式のように表すことができます。
吸着平衡においては吸着速度と脱着速度が等しいので、
$$k_{a}p(1-θ)=k_{d}θ$$
$$θ=\frac{(k_{a}/k_{d})p}{1+(k_{a}/k_{d})p}・・・(4)$$
(4)式となります。
ここで、吸着平衡定数Kを、
$$K=\frac{k_{a}}{k_{d}}・・・(5)$$
(5)式とします。
また、吸着量qは飽和吸着量q∞に吸着サイトの割合θをかけたものなので、
$$q=q_{∞}θ・・・(6)$$
(6)式となります。
(5)、(6)式を(4)式に代入し整理すると、
$$q=\frac{q_{∞}Kp}{1+Kp}・・・(1)$$
冒頭の(1)式が得られ、Langmuirの吸着等温式を導出できました。
Langmuirプロット
吸着平衡実験を行なった場合に、得られるデータは吸着量qとそのときの分圧pです。
これらのデータから(1)式のパラメータq∞とKを決定しますが、(1)式が非線形だとフィッティングしにくいです。
そこで、(1)式を変形し線形化した式をグラフにプロットすると、より簡単にパラメータを決定できます。これをLangmuirプロットといいます。
(1)式を両辺逆数を取ると、
$$\frac{1}{q}=\frac{1}{q_{∞}K}\frac{1}{p}+\frac{1}{q_{∞}}・・・(7)$$
(7)式あるいは
$$\frac{p}{q}=\frac{1}{q_{∞}K}+\frac{p}{q_{∞}}・・・(8)$$
(8)式となります。
(7)式では縦軸1/q、横軸1/p、(8)式では縦軸p/q、横軸pとしてプロットすればy=ax+bの形の線形の式になります。
計算例
例として、以下に示す条件下でLangmuirプロットをやってみましょう。
| 濃度p [g/m3] | 吸着量q [g/g] | 1/p | 1/q | p/q |
| 0.451 | 0.316 | 2.217 | 3.165 | 1.427 |
| 0.793 | 0.327 | 1.261 | 3.058 | 2.425 |
| 1.240 | 0.338 | 0.806 | 2.959 | 3.669 |
| 1.910 | 0.350 | 0.524 | 2.857 | 5.457 |
| 2.410 | 0.335 | 0.415 | 2.985 | 7.194 |
| 2.660 | 0.356 | 0.376 | 2.809 | 7.472 |
| 2.990 | 0.358 | 0.334 | 2.793 | 8.352 |
吸着平衡実験により、実験したときの分圧(もしくは濃度)pとそのときの吸着量qが得られます。
今回は(7)、(8)式両方プロットしてみますので、pとqから1/p、1/q、p/qをそれぞれ算出すると上の表の値になります。
それぞれLangmuirプロットすると、
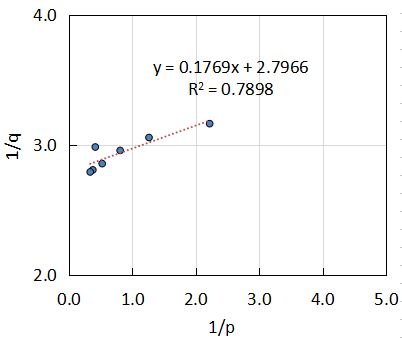
(7)式のLangmuirプロット
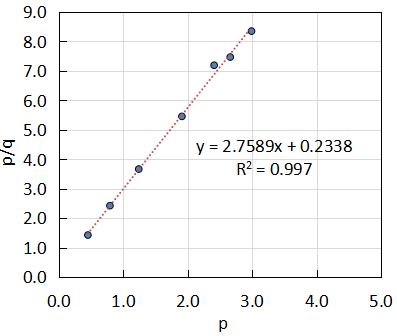
(8)式のLangmuirプロット
上のグラフになります。
表計算ソフトで近似直線を引きましたが、(7)式はR2が0.7898と悪く、(8)式の方が良い相関が得られました。
(7)式から、
$$\frac{1}{q_{∞}K}=0.1769・・・(9)$$
$$\frac{1}{q_{∞}}=2.7966・・・(10)$$
(8)式から、
$$\frac{1}{q_{∞}K}=0.2338・・・(11)$$
$$\frac{1}{q_{∞}}=2.7589・・・(12)$$
が近似直線より得られます。それぞれq∞とKを求めると、
- (7)式:q∞=0.358、K=15.808
- (8)式:q∞=0.362、K=11.798
となり、式により多少の差異が生じます。線形プロットしたときのR2から考えると、(8)式の方が精度が良さそうです。
おわりに
Langmuirの吸着等温式について解説しました。
大学のテストや資格試験では、Langmuirプロットによる計算問題は出題されやすいため、ぜひ覚えておきましょう。
