概要
フィルターの繊維1本が粒子をどの程度捕集するかを表わす効率を単一繊維捕集効率といいます。
フィルターの総合的な捕集効率を算出するためには、この単一繊維捕集効率が重要になってきます。
単一繊維捕集効率は粒子の大きさやフィルター繊維径、充填率の値によって大きく変化します。
したがって、現在に至るまで様々な条件下での計算式が発表されており、計算式があまり統一されていないようです。
自分が計算したい条件に適用できる式を選ぶことが重要でしょう。
単一繊維捕集効率ηt
単一繊維捕集効率ηt[-]は、様々な捕集機構による捕集効率の和と付着効率ηAの積で表されます。
$$η_{t}=(η_{I}+η_{R}+η_{D}+η_{G})η_{A}・・・(1)$$
ηI:慣性捕集効率[-]、ηR:さえぎり捕集効率[-]、ηD:拡散捕集効率[-]
ηG:重力捕集効率[-]、ηA:付着効率[-]
どの捕集機構が支配的かは、捕集する粒子径や流速、繊維径によって変化します。
慣性捕集効率ηI
粒子径が大きくなると、慣性によって粒子は流体の流れに追随できなくなります。
粒子を含む流体がフィルター内を通過するとき、流体はそのまま通過しますが、粒子はフィルターの繊維に衝突することで捕集されます。
このような捕集原理を慣性捕集機構といいます。
粒子径が数μm以上の大きさになると、慣性捕集機構が支配的となります。
詳細は以下の記事で解説しています。
-

【慣性捕集機構】について解説:慣性力による粒子の捕集
粒子を含む流体中にフィルター等の障害物を設置すると、流体は障害物を避けて流れますが、粒子は障害物を避けきれずに衝突し捕集されます。このような慣性力を利用した捕集機構を慣性捕集機構といいます。
続きを見る
さえぎり捕集効率ηR
慣性力が働かない大きさまで粒子が小さくなると、粒子は流体と同じ流線を辿ります。
ただし、粒子と流体分子の大きさは異なります。
繊維近傍の流れにおいて、流体分子なら通過できる流線であっても、粒子は大きいので繊維に遮られるような形で接触して捕集されます。
このような捕集原理をさえぎり捕集機構といいます。
詳細は以下の記事で解説しています。
-

【さえぎり捕集機構】について解説:障害物による粒子のさえぎり
粒子が小さくなると慣性力が働きにくくなり、粒子は流体と同じ運動をするようになります。障害物近傍を通過するとき、ガス分子は通過できますが、粒子は障害物に物理的にさえぎられて捕集されます。この捕集機構をさえぎり捕集機構といいます。
続きを見る
拡散捕集効率ηD

粒子がさらに小さくなると、粒子は流体の流れに追随しつつ、ブラウン運動によりランダムな動きをするようになります。
繊維近傍においては、このランダムな動きにより繊維と衝突し捕集されます。
このような捕集原理を拡散捕集機構といいます。
詳細は以下の記事で解説しています。
-

【拡散捕集機構】について解説:ブラウン拡散による粒子捕集
粒子が非常に小さくなると、ランダムな軌道で運動するようになります。これをブラウン運動といい、この運動により粒子を捕集する機構を拡散捕集機構といいます。拡散捕集は小さな粒子を捕集する場合の支配的な機構です。
続きを見る
重力捕集効率ηG
粒子は当然ですが、重力の影響を受けます。
ある程度大きい粒子になると重力の影響が大きくなり、粒子が繊維と衝突し捕集されるようになります。
重力による捕集効率ηG[-]は、流体の流れと重力の方向によって変化します。
$$上下流:η_{G}=\frac{G}{1+G}・・・(2)$$
$$水平流:η_{G}=\frac{G}{\sqrt{1+G^2}}・・・(3)$$
$$G=\frac{C_{c}ρ_{p}{d_{p}}^{2}g}{18μu}・・・(4)$$
G:重力パラメータ[-]、Cc:カニンガムの補正係数[-]、ρp:粒子密度[kg/m3]
dp:粒子径[m]、g:重力加速度[m/s2]、流体粘度[Pa・s]、u:流速[m/s]
粒子径が小さいと重力の影響はほとんど無視できます。
吸着効率ηA
液滴の場合は繊維に接触すると100%吸着されると考えてよいですが、固体粒子の場合は繊維表面で粒子が滑り捕集されないことがあります。
特に粒子径が大きくなると滑りの影響が大きくなります。
この吸着効率ηA[-]についてはあまり多くの知見がないですが、有名なのはPtakとJaroszczykの(5)式です。
$$η_{A}=\frac{190}{(Re_{p}・Stk)^{0.68}+190}・・・(5)$$
$$Re_{p}=\frac{ρ_{p}ud_{p}}{μ}・・・(6)$$
$$Stk(直径基準)=\frac{C_{c}ρ_{p}u{d_{p}}^{2}}{18μd_{f}}・・・(7)$$
$$Re_{f}=\frac{ρud_{f}}{μ}・・・(8)$$
Rep:粒子レイノルズ数[-]、Stk:ストークス数[-]、Ref:繊維レイノルズ数[-]
df:繊維径[m]
(5)式は1<Stk<120、0.4<Ref<5.75で精度が良いとされています。
単一繊維捕集効率の粒子径依存性
単一繊維捕集効率ηtを粒子径に対してプロットしたものを下図に示します。
- α=0.1
- df=10μm
- u=0.01m/s
- 流体:空気
- T=298K
- P=760mmHg
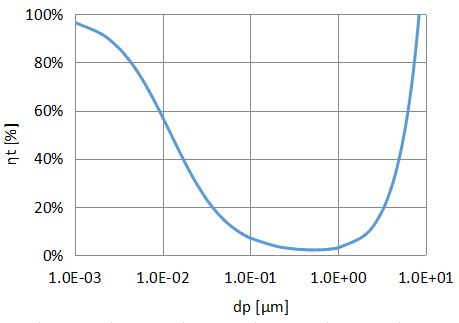
粒子径が小さくなるほど拡散捕集が支配的となり、捕集されやすくなります。
逆に粒子径が大きくなるほど慣性捕集が支配的となり捕集されやすくなります。
この結果、拡散捕集と慣性捕集の両方があまり働かない粒子径の領域が生じます。上図の結果だと、0.1~1.0μm程度の粒子が捕集されにくいと言えます。
この捕集されにくい領域の粒子を捕集するためには、繊維径を細くする、フィルターの充填厚さを厚くする等が有効です。
ただし、圧力損失が大きく増加するため、プロセス上許容できるか注意が必要です。
まとめ
単一繊維捕集効率について解説しました。
捕集したい粒子径により支配的な捕集機構が変化します。
場合によっては1つの装置で全ての粒子径を捕集せずに、多段にして役割分担させるのが良いかもしれません。



