概要
本記事ではPythonのif文を使用した計算例として、配管流れの摩擦係数f(管摩擦係数)の適用範囲による使い分け計算を解説しています。
化学工学や流体力学で使用される経験式や実験式はパラメータの適用範囲が定められていることが多く、パラメータの値によって使用する式を使い分ける必要があります。
今回はレイノルズ数Reによって式の適用範囲が異なっている摩擦係数fの計算をif文でやってみます。
計算の前提条件
上の記事で解説しているファニングの式等で使用する摩擦係数fを計算してみます。
配管内流れでは層流域において
$$f=\frac{16}{Re}・・・(1)$$
f:摩擦係数[-]、Re:レイノルズ数[-]
$$Re<2100$$
(1)式で表されます。
一方で乱流域では(2)式のBlasiusの式が有名です。
$$f=0.0791Re^{-0.25}・・・(2)$$
$$3×10^{3}<Re<10^{5}$$
(1),(2)式をレイノルズ数Reによって使う式を切り替えるようにPythonで記述し、それぞれグラフでプロットするところまでやってみましょう。
Pythonでの計算法
ライブラリ・モジュールのインポート
Pythonでグラフを作成しますのでMatplotlibをインポートします。
#Matplotlibインポート
import matplotlib.pyplot as plt初期条件の入力
レイノルズ数の初期条件を入力します。とりあえずRe=100くらいからスタートして適当な刻みで増やしていきます。
(1)式と(2)式でレイノルズ数の適用範囲が異なることから、レイノルズ数の刻み幅をそれぞれの式で変えようと思いますが後で設定します。
#初期条件
Re=100その他計算条件の入力
繰り返し計算回数imaxを入力します。とりあえず100回くらいにしておきます。
#その他計算条件
imax=100グラフ作成用の配列入力
(1)式用と(2)式用で合計4つの空の配列を用意します。
#グラフ作成用
gRe1 = []
gRe2 = []
gf1 = []
gf2 = []方程式定義
(1),(2)式をそれぞれ定義します。
#方程式定義
def f1(Re):
return 16/Re
def f2(Re):
return 0.0791*Re**(-0.25)繰り返し計算の入力
レイノルズ数を指定の刻み幅で増やしてその都度摩擦係数fを計算する操作を繰り返します。
ただし、ずっと同じ刻み幅だとデータ数が多くなってしまいます。(1),(2)式の適用範囲を考えると、(1)式の適用範囲では刻み幅h=100とし、(2)式の適用範囲ではh=1000とします。
#繰り返し計算
for i in range(imax):
if Re < 2100:
f=f1(Re)
gRe1.append(Re)
gf1.append(f)
h=100
elif 2100 <=Re <3100:
f=0
else:
f=f2(Re)
gRe2.append(Re)
gf2.append(f)
h=1000
print('i:{0:4d}, Re:{1:6}, f:{2:7.3f}' .format(i,Re,f))
Re=Re+h3行目からif文の入力を行なっています。
Re<2,100の場合には、4~7行目の操作を行なうように入力しています。
4行目で(1)式を使用するように入力、5行目でReの計算値をgRe1配列に格納、6行目でfの計算値をgf1配列に格納、7行目で刻み幅を100に設定します。
9行目でelifを使用して2,100≦Re<3,100の区間の設定をしています。
この区間は流れの遷移域であり、流れが予測し難い領域です。(1),(2)式のどちらも適用範囲外であるため、この区間ではappend関数を入力せず配列に値を取得しないようにします。
摩擦係数fは値を取得しないのでどんな値でも関係ありませんが、ここではf=0としておきます。
12行目でelseを使用して前述したレイノルズ数以外の値を取る場合には、13~16行目の操作を行なうように入力しています。
13行目で(2)式を使用するように入力、 14行目でReの計算値をgRe2配列に格納、15行目でfの計算値をgf2配列に格納、16行目で刻み幅を1000に設定します。
18行目でprint関数で計算値の出力、19行目でレイノルズ数Reの更新をしています。
グラフの出力
最後にグラフの出力設定をします。
#グラフ出力
plt.plot(gRe1, gf1)
plt.plot(gRe2, gf2)
plt.xscale('log') # x軸を対数プロット
plt.yscale('log') # y軸を対数プロット
plt.xlabel('Re [-]')
plt.ylabel('f [-]')
plt.legend(['f1', 'f2'])
plt.show()2行目で横軸gRe1、縦軸gf1のグラフをプロットし、3行目で横軸gRe2、縦軸gf2のグラフをプロットします。
また、もともと摩擦係数fとレイノルズ数Reのグラフは両対数でプロットされることが多いので、本記事でもそれに倣います。
4,5行目でx軸とy軸を対数プロットにして両対数とします。
6行目でx軸のラベル、7行目でy軸のラベル、8行目で凡例を入力します。
計算結果の確認
特に入力ミス等がなければ計算結果が以下のように表示されます。
i: 0, Re: 100, f: 0.160
i: 1, Re: 200, f: 0.080
i: 2, Re: 300, f: 0.053
i: 3, Re: 400, f: 0.040
i: 4, Re: 500, f: 0.032
i: 5, Re: 600, f: 0.027
i: 6, Re: 700, f: 0.023
i: 7, Re: 800, f: 0.020
i: 8, Re: 900, f: 0.018
i: 9, Re: 1000, f: 0.016
i: 10, Re: 1100, f: 0.015
i: 11, Re: 1200, f: 0.013
i: 12, Re: 1300, f: 0.012
i: 13, Re: 1400, f: 0.011
i: 14, Re: 1500, f: 0.011
i: 15, Re: 1600, f: 0.010
i: 16, Re: 1700, f: 0.009
i: 17, Re: 1800, f: 0.009
i: 18, Re: 1900, f: 0.008
i: 19, Re: 2000, f: 0.008
i: 20, Re: 2100, f: 0.000
i: 21, Re: 2200, f: 0.000
i: 22, Re: 2300, f: 0.000
i: 23, Re: 2400, f: 0.000
i: 24, Re: 2500, f: 0.000
i: 25, Re: 2600, f: 0.000
i: 26, Re: 2700, f: 0.000
i: 27, Re: 2800, f: 0.000
i: 28, Re: 2900, f: 0.000
i: 29, Re: 3000, f: 0.000
i: 30, Re: 3100, f: 0.011
i: 31, Re: 4100, f: 0.010
i: 32, Re: 5100, f: 0.009
i: 33, Re: 6100, f: 0.009
i: 34, Re: 7100, f: 0.009
i: 35, Re: 8100, f: 0.008
i: 36, Re: 9100, f: 0.008
i: 37, Re: 10100, f: 0.008
i: 38, Re: 11100, f: 0.008
i: 39, Re: 12100, f: 0.008
i: 40, Re: 13100, f: 0.007
i: 41, Re: 14100, f: 0.007
i: 42, Re: 15100, f: 0.007
i: 43, Re: 16100, f: 0.007
i: 44, Re: 17100, f: 0.007
i: 45, Re: 18100, f: 0.007
i: 46, Re: 19100, f: 0.007
i: 47, Re: 20100, f: 0.007
i: 48, Re: 21100, f: 0.007
i: 49, Re: 22100, f: 0.006
i: 50, Re: 23100, f: 0.006
i: 51, Re: 24100, f: 0.006
i: 52, Re: 25100, f: 0.006
i: 53, Re: 26100, f: 0.006
i: 54, Re: 27100, f: 0.006
i: 55, Re: 28100, f: 0.006
i: 56, Re: 29100, f: 0.006
i: 57, Re: 30100, f: 0.006
i: 58, Re: 31100, f: 0.006
i: 59, Re: 32100, f: 0.006
i: 60, Re: 33100, f: 0.006
i: 61, Re: 34100, f: 0.006
i: 62, Re: 35100, f: 0.006
i: 63, Re: 36100, f: 0.006
i: 64, Re: 37100, f: 0.006
i: 65, Re: 38100, f: 0.006
i: 66, Re: 39100, f: 0.006
i: 67, Re: 40100, f: 0.006
i: 68, Re: 41100, f: 0.006
i: 69, Re: 42100, f: 0.006
i: 70, Re: 43100, f: 0.005
i: 71, Re: 44100, f: 0.005
i: 72, Re: 45100, f: 0.005
i: 73, Re: 46100, f: 0.005
i: 74, Re: 47100, f: 0.005
i: 75, Re: 48100, f: 0.005
i: 76, Re: 49100, f: 0.005
i: 77, Re: 50100, f: 0.005
i: 78, Re: 51100, f: 0.005
i: 79, Re: 52100, f: 0.005
i: 80, Re: 53100, f: 0.005
i: 81, Re: 54100, f: 0.005
i: 82, Re: 55100, f: 0.005
i: 83, Re: 56100, f: 0.005
i: 84, Re: 57100, f: 0.005
i: 85, Re: 58100, f: 0.005
i: 86, Re: 59100, f: 0.005
i: 87, Re: 60100, f: 0.005
i: 88, Re: 61100, f: 0.005
i: 89, Re: 62100, f: 0.005
i: 90, Re: 63100, f: 0.005
i: 91, Re: 64100, f: 0.005
i: 92, Re: 65100, f: 0.005
i: 93, Re: 66100, f: 0.005
i: 94, Re: 67100, f: 0.005
i: 95, Re: 68100, f: 0.005
i: 96, Re: 69100, f: 0.005
i: 97, Re: 70100, f: 0.005
i: 98, Re: 71100, f: 0.005
i: 99, Re: 72100, f: 0.005
i: 100, Re: 73100, f: 0.005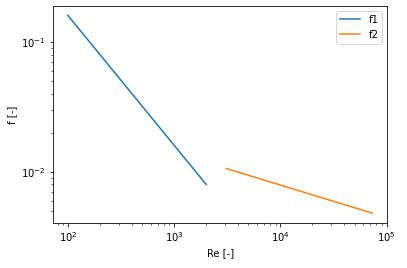
計算結果が数字とグラフの両方で表示されます。
Re<2,100までの領域が(1)式で計算されてf1(青色)でプロットされ、3,100<Reの領域が(2)式で計算されてf2(オレンジ色)でプロットできました。
このように摩擦係数fは層流か乱流かで使う式や値が異なってきますので注意しましょう。
下に計算コードを最初から最後までまとめて載せておきます。
#Matplotlibインポート
import matplotlib.pyplot as plt
#初期条件
Re=100
#Re2=3000
#その他計算条件
imax=101
#グラフ作成用
gRe1 = []
gRe2 = []
gf1 = []
gf2 = []
#方程式定義
def f1(Re):
return 16/Re
def f2(Re):
return 0.0791*Re**(-0.25)
#繰り返し計算
for i in range(imax):
if Re < 2100:
f=f1(Re)
gRe1.append(Re)
gf1.append(f)
h=100
elif 2100 <=Re <3100:
f=0
else:
f=f2(Re)
gRe2.append(Re)
gf2.append(f)
h=1000
print('i:{0:4d}, Re:{1:6}, f:{2:7.3f}' .format(i,Re,f))
Re=Re+h
#グラフ出力
plt.plot(gRe1, gf1)
plt.plot(gRe2, gf2)
plt.xscale('log') # x軸を対数プロット
plt.yscale('log') # y軸を対数プロット
plt.xlabel('Re [-]')
plt.ylabel('f [-]')
plt.legend(['f1', 'f2'])
plt.show()まとめ
Pythonでif文を使用して摩擦係数fの計算を解説しました。
パラメータによる条件分岐が出来ると、より楽に計算できるようになりますので覚えておきましょう。

