概要
本記事ではPythonのラグランジュ補間を使用した計算例として、気液平衡曲線(アンモニア-水)の補間を行ないました。
ラグランジュ補間でやる必要性はなく、近似式・補間式を作れるなら手法は何でもいいと思いますが例としてちょうど良さそうなのでやってみます。
計算条件
$$(x_{1},y_{1})=(0.0125,0.0151)$$
$$(x_{2},y_{2})=(0.0166,0.0201)$$
$$(x_{3},y_{3})=(0.0207,0.0253)$$
$$(x_{4},y_{4})=(0.0257,0.0320)$$
$$(x_{5},y_{5})=(0.0307,0.0389)$$
$$(x_{6},y_{6})=(0.0406,0.0528)$$
$$(x_{7},y_{7})=(0.0502,0.0671)$$
$$(x_{8},y_{8})=(0.0735,0.1040)$$
アンモニア-水の気液平衡データが上のように与えられているとします。xは液相のアンモニア組成[-]、yは気相のアンモニア組成[-]です。
データとしては全体的にアンモニアが微小な領域のものとなります。アンモニアを水に吸収させて廃ガス処理をするような除害塔の設計条件に近いですね。
今回の条件のような吸収成分の濃度が低い場合はHenryの法則が適用でき、xy線図の気液平衡線の傾きが直線近似できるようになります。
ただし、吸収成分の濃度が高くなるにつれて気液平衡線が曲線になるため、除害塔の入口廃ガス中の吸収成分濃度が高いとHenryの法則による直線近似のみで計算することはできなくなります。
そこで、今回のように実測データがある場合には直線領域と曲線領域の両方を含めた補間式を作成することで低濃度~高濃度まで対応できるようになります。
Pythonでの計算法
ライブラリ・モジュールのインポート
Pythonでグラフを作成しますのでMatplotlibをインポートします。
#ライブラリインポート
import matplotlib.pyplot as plt前提条件の入力
アンモニアの液相組成と気相組成のデータをリストにしてそれぞれ入力します。
また、データの点数が後々必要となるので入力します。
#前提条件
x_lis=[0.0125,0.0166,0.0207,0.0257,0.0307,0.0406,0.0502,0.0735]
y_lis=[0.0151,0.0201,0.0253,0.032,0.0389,0.0528,0.0671,0.104]
m=8 # データ点数初期条件の入力
ラグランジュ補間計算時のxの初期値を入力します。
前提条件ではx=0.0125が最小値ですから、x=0.01くらいからスタートするものとしました。
#初期値
xm=0.01 #補間計算時の初期値その他計算条件の入力
ラグランジュ補間計算時のデータ点数と刻み幅を設定しました。
#その他計算条件
n=71 # 補間計算のデータ点数
h=0.001 # 刻み幅グラフ作成用の配列入力
補間計算値であるxとyを格納する空の配列を用意しました。
#グラフ作成用
gx=[]
gly=[]ラグランジュ補間式定義
ラグランジュ補間については下の記事で説明しています。
ラグランジュ補間は(1)式で表され、この式をPythonで記述します。
$$\begin{align}y&=y_{1}\frac{(x-x_{2})(x-x_{3})・・・(x-x_{n})}{(x_{1}-x_{2})(x_{1}-x_{3})・・・(x_{1}-x_{n})}+ y_{2}\frac{(x-x_{1})(x-x_{3})・・・(x-x_{n})}{(x_{2}-x_{1})(x_{2}-x_{3})・・・(x_{2}-x_{n})}+\\&・・・+y_{n}\frac{(x-x_{1})(x-x_{2})・・・(x-x_{n-1})}{(x_{n}-x_{1})(x_{n}-x_{2})・・・(x_{n}-x_{n-1})}・・・(1)\end{align}$$
#ラグランジュ補間式定義
def f(i, x):
A=1
for j in range(len(x_lis)):
if j != i :
A=A*(x-x_lis[j])/(x_lis[i]-x_lis[j])
return A
def flag(x,m):
B=0
for j in range(m):
B=B+y_lis[j]*f(j, x)
return Bまずは(1)式のxを含む掛け算部分
$$\frac{(x-x_{1})(x-x_{2})・・・(x-x_{n-1})}{(x_{n}-x_{1})(x_{n}-x_{2})・・・(x_{n}-x_{n-1})}$$
を2~7行目で入力しています。
ポイントは5行目のif文で、jとiが同じ数字でないときだけ掛け算を計算するようにしている点です。j=iのときを含めてしまうとゼロ割になってしまいますので。
次に9~13行目で
$$y_{n}×A$$
を計算させ、m=8回繰り返すことで8つの多項式を足し合わせています。
この辺の式の記述はこちらのサイト様のものを参考にさせていただきました。自力で思いつくのはなかなか難しく、先人の知恵をお借りしました。
繰り返し計算の入力
先ほど定義した補間式を使用して、"その他計算条件"で指定した条件でfor文の繰り返し計算を入力します。
#繰り返し計算
for j in range(n):
gx.append(xm)
gly.append(flag(gx[j],m))
xm=xm+h3行目でxmを配列gxに格納します。
4行目で定義した補間式flag(x,m)のxにgx[j]を代入して計算させ、結果を配列glyに格納します。
5行目でxmの値を更新します。
グラフの出力
最後にグラフの出力設定をします。
#グラフ出力
plt.plot(x_lis, y_lis,'o')
plt.plot(gx, gly,'-')
plt.xlabel('x [-]')
plt.ylabel('y [-]')
plt.legend(['Row data','Lagrange'])
plt.show()2行目で元データのグラフをプロットし、3行目でラグランジュ補間のグラフをプロットします。
4行目でx軸のラベル、5行目でy軸のラベル、6行目で凡例を入力します。
計算結果の確認
特に入力ミス等がなければグラフが以下のように表示されます。
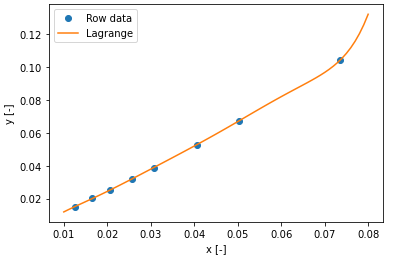
元データの内挿範囲ではきれいに補完できていますね。一方でx=0.075を超える外挿範囲になってくると急激に傾きが大きくなっており妥当性が疑われます。
もともとの気液平衡関係から考えると、傾きが大きくなってもおかしくはないのでたまたま実現象と合っている可能性はありますが、実測データ等できちんと確認した方がよいです。
下に計算コードを最初から最後までまとめて載せておきます。
#ライブラリインポート
import matplotlib.pyplot as plt
#前提条件
x_lis=[0.0125,0.0166,0.0207,0.0257,0.0307,0.0406,0.0502,0.0735]
y_lis=[0.0151,0.0201,0.0253,0.032,0.0389,0.0528,0.0671,0.104]
m=8 # データ点数
#初期値
xm=0.01 #補間計算時の初期値
#その他計算条件
n=71 # 補間計算のデータ点数
h=0.001 # 刻み幅
#グラフ作成用
gx=[]
gly=[]
#ラグランジュ補間式定義
def f(i, x):
A=1
for j in range(len(x_lis)):
if j != i :
A=A*(x-x_lis[j])/(x_lis[i]-x_lis[j])
return A
def flag(x,m):
B=0
for j in range(m):
B=B+y_lis[j]*f(j, x)
return B
#繰り返し計算
for j in range(n):
gx.append(xm)
gly.append(flag(gx[j],m))
xm=xm+h
#グラフ出力
plt.plot(x_lis, y_lis,'o')
plt.plot(gx, gly,'-')
plt.xlabel('x [-]')
plt.ylabel('y [-]')
plt.legend(['Row data','Lagrange'])
plt.show()Scipyによる簡略化
ラグランジュ補間は有名なのでライブラリによる簡略化ができます。
Scipyをインポートし、lagrange関数を使用することで簡単にラグランジュ補間することができます。
#Matplotlibインポート
from scipy.interpolate import lagrange
import numpy as np
import matplotlib.pyplot as plt
#前提条件
x_lis=[0.0125,0.0166,0.0207,0.0257,0.0307,0.0406,0.0502,0.0735]
y_lis=[0.0151,0.0201,0.0253,0.032,0.0389,0.0528,0.0671,0.104]
#補間式定義
x=np.linspace(0.01,0.08,num=71)
f_lag=lagrange(x_lis,y_lis)
#グラフ出力
plt.plot(x_lis, y_lis,'o')
plt.plot(x, f_lag(x),'-')
plt.xlabel('x [-]')
plt.ylabel('y [-]')
plt.legend(['Row data','Lagrange'])
plt.show()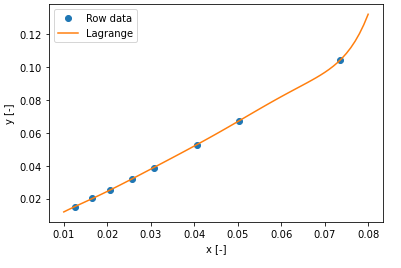
まったく同じ結果となりました。便利ですね。
まとめ
Pythonでのラグランジュ補間の計算例として、アンモニア-水の気液平衡曲線の補間をやりました。
慣れてくればScipyで簡単に補間する方が時間短縮できます。

