概要
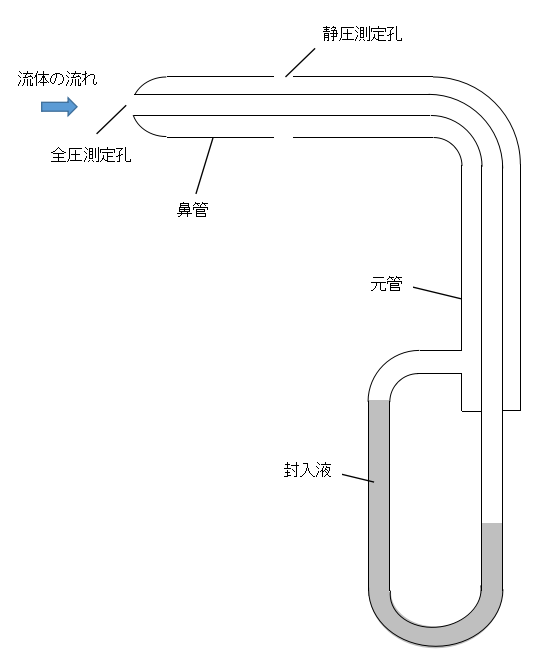
上図のように全圧と静圧を測定することで流体の流速を測定する装置をピトー管といいます。
測定した全圧と静圧から動圧を算出することができます。この計算はベルヌーイの定理から導くことができ、動圧は流速の2乗に比例することが知られています。
したがって、測定する流速が小さいと誤差が大きくなりやすく、低流速の測定には向いていません。
また、流れの方向とピトー管の軸が一致している必要があり、流れが複雑になっている箇所では正しく測定できません。
工場では、主に配管内を流れる流体の流速を測定するのにピトー管は便利です。
ピトー管の測定原理

上図にピトー管で円管内の流速を測定する場合の概要図を示します。
ピトー管の先端部はよどみ点となっており、流速がゼロとなる箇所です。
動圧がゼロなので、よどみ点では全圧=静圧となります。
一方で、ピトー管のU字部には流体に不溶な液体が封入されており、ピトー管のもう片方は配管に接続されています。
このとき、ピトー管の両端でベルヌーイの式を立てると、
$$p_{0}=p+\frac{1}{2}ρ_{1}v^{2}・・・(1)$$
ρ1:測定流体の密度[kg/m3]
(1)式が成り立ちます。(1)式を変形すると、流速vは、
$$v=\sqrt{\frac{2}{ρ_{1}}(p_{0}-p)}・・・(2)$$
(2)式で表されます。
したがって、全圧p0と静圧pの差を求めることができれば流速が算出できます。
次に、ピトー管の封入液体に注目します。
この封入液体はピトー管の両端の静圧差によって、上図のように液柱高さに差が生じます。
封入液体の両端の静圧をp0'、p'とすると、
$$p_{0}=p_{0}'+ρ_{1}gz_{1}・・・(3)$$
$$p=p'+ρ_{1}gz_{2}・・・(4)$$
g:重力加速度[m/s2]
(3)、(4)式が成り立ちます。
また、封入液体の両端の静圧差は、
$$p_{0}'-p'=ρ_{2}g(z_{2}-z_{1})・・・(5)$$
ρ2:封入流体の密度[kg/m3]
(5)式となります。
(3)~(5)式から、
$$\begin{align}p_{0}-p&=p_{0}'-p'-ρ_{1}g(z_{2}-z_{1})\\&=(ρ_{2}-ρ_{1})g(z_{2}-z_{1})\end{align}・・・(6)$$
(15)式となります。
(6)式を(2)式に代入することで、
$$v=\sqrt{\frac{2}{ρ_{1}}(ρ_{2}-ρ_{1})g(z_{2}-z_{1})}・・・(7)$$
(7)式となり、ピトー管の液柱の読み値と物性値から流速を算出することができます。
おわりに
ピトー管について解説しました。
ピトー管の測定原理は資格試験等に出題されやすく、覚えておくと役立つ場面が多いです。
