【Python】最急降下法の解説：回分操作コストの最小化計算

概要

本記事では非線形最小二乗法の計算手法の1つである最急降下法について解説します。

他の手法と比較して簡単に計算できますが、繰り返し計算回数が多くなり計算時間がかかるのが欠点です。

化学工学では何らかの関数の最小値を求めることはよくあります。実験データのフィッティングやコスト計算が特に多いでしょうか。

表計算ソフトのソルバー機能で簡単に収束するうちはよいですが、いずれは簡単に収束しない課題にぶち当たることでしょう。

そのため、非線形の最小二乗法の解法についてある程度体系的に学んでおくことは意味があると思います。

原理

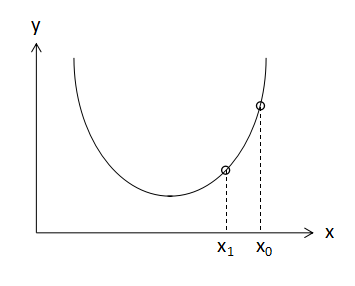
上図のようなy=f(x)で表される関数の最小値を算出するとします。

最急降下法とは勾配法とも呼ばれ、関数f(x)の勾配、すなわち一次導関数f'(x)を使用して最小値を求めます。

ある初期値x₀からスタートすると、 x₀における一次微分はf'(x₀)となります。

このf'(x₀)に学習率αと呼ばれる値をかけ、次の値x₁は、

$$x_{1}=x_{0}-αf'(x_{0})・・・(1)$$

(1)式で表されます。学習率αは0<α<1となる値をユーザーが設定します。試しに何回か計算してみてうまく収束する値を選びましょう。

あとは(1)式の操作を繰り返し、f(x)の値がほとんど変わらなくなれば収束したとみなせます。

(1)式を一般化すると、

$$x_{n+1}=x_{n}-αf'(x_{n})・・・(2)$$

(2)式となります。

Pythonでの計算法

この手の界隈では有名な回分操作のコスト計算問題を最急降下法で解いてみましょう。

計算条件

回分反応器で有機化合物の生産を行ないます。このときの年間総コストの最小値C_Tmin[$/y]と、最小となる回分操作の1サイクルにかかる時間t_min[h/cycle]を求めましょう。

回分操作1サイクルにかかる時間t[h/cycle]は、

$$運転時間：1.5x^{0.25} [h]$$

x：1バッチ当たりの生産量[kg/cycle]

$$準備時間：1.4 [h/cycle]$$

運転時間と準備時間を足して、

$$t=1.5x^{0.25}+1.4・・・(3)$$

(3)式で表されるものとします。

また、装置の年間固定費C_f[$/y]は

$$C_{f}=340x^{0.8}・・・(4)$$

(4)式で表されるとします。

その他前提条件は、以下に示す通りです。

運転期間のコスト：20[$/h]
準備期間のコスト：15[$/h]
年間生産量：1,000,000[kg/y]
原材料費とその他諸経費：260,000[$/y]

目的関数の作成

非線形最小二乗法を数学の問題として解く場合と化学工学の実務として解く場合とで最も異なる点は、目的関数を状況に応じて作成する必要があることです。

(3)式から運転期間+準備期間のコストC_p[$/cycle]は、

$$C_{p}=1.5x^{0.25}×20+1.4×15・・・(5)$$

(5)式となります。

加えて年間固定費C_AF[$/y]は(4)式から、

$$C_{AF}=340x^{0.8}+260000・・・(6)$$

(6)式となります。

また、1年間のサイクル数N_c[cycle/y]は、

$$N_{c}=\frac{1000000}{x}・・・(7)$$

(7)式となります。したがって年間の総コストC_T[$/y]は、

$$C_{T}=C_{p}×N_{c}+C_{AF}=(30x^{0.25}+21)\frac{1000000}{x}+340x^{0.8}+260000・・・(8)$$

(8)式となります。この(8)式のC_Tが最小となるような1バッチ当たりの生産量xを決定し、(3)式から1サイクルにかかる時間を算出します。

ライブラリ・モジュールのインポート

ここからPythonでの記述となります。こちらのサイト様の記事を参考にさせていただきました。

NumpyとMatplotlibをインポートします。

#モジュールインポート
import numpy as np
import matplotlib.pyplot as plt

前提条件

問題で与えられた前提条件を入力します。

#前提条件
cop=20  #運転期間のコスト[$/h]
cpp=15  #準備期間のコスト[$/h]
P=1000000  #年間生産量[kg/y]
raw=260000  #原材料費とその他諸経費[$/y]

目的関数

(8)式の目的関数をdef文で定義します。

目的関数
def f(x):
    opcost=cop*1.5*x**0.25+cpp*1.4  #(5)式
    return opcost*P/x+340*x**0.8+raw

偏微分と勾配の計算

元の記事を大いに参考にさせていただきました。

このような記述を自力で書けるようになれば良いのですが、数学や化学工学にはないPython特有の文法の壁があってなかなか難しいところです。

今回の問題は変数が1つしかありませんが、変数が2つ以上ある場合でも偏微分して対応できるコードになっています。

#偏微分と勾配の計算
def numerical_diff(f, x, i):
    h=1e-4
    h_vec=np.zeros_like(x)
    h_vec[i]=h
    return (f(x+h_vec)-f(x-h_vec))/(2*h)  #数値微分

def numerical_gradient(f, x):
    grad=np.zeros_like(x)
    for i, _ in enumerate(x):
        grad[i]=numerical_diff(f, x, i)
    return grad

最急降下法の入力

メインの最急降下法を入力します。

#最急降下法
def gradient_descent(f, initial_position, learning_rate=0.1, steps=1000):
    x=initial_position
    for _ in range(steps):
        grad=numerical_gradient(f, x)
        x -= learning_rate * grad
    return x

今回は学習率(learning_rate)を0.1としてうまくいきましたが、うまくいかなければ値をいろいろ変えてみましょう。

6行目がPython特有の記述で、これは

$$x=x-learing rate×grad$$

を意味し(2)式を表わしています。

最急降下法の実行と出力

定義した最急降下法の実行と出力を記述しています。

#最急降下法の実行と出力
def main():
    min_pos = gradient_descent(f,[1000])  #最急降下法の実行
    CTmin=f(min_pos)  #(8)式
    tmin=1.5*min_pos**0.25+1.4  #(3)式
    print('総コストが最小となる1バッチ当たりの生産量[kg/cycle]: {0}'.format(min_pos))
    print('総コスト最小値[$/y]: {0}'.format(CTmin))
    print('総コストが最小となる場合の1サイクルにかかる時間[h/cycle]: {0}'.format(tmin))
main()  #関数の実行

3行目で最急降下法を実行しています。初期値は1,000としていますが、もしうまく収束しない場合はいろいろ変えてみましょう。

4行目で(8)式を使用して総コストの最小値を計算しています。

5行目で(3)式を使用して総コストが最小となる場合の1サイクルにかかる時間を計算しています。

最小値確認のためのグラフ作成

最急降下法の計算は上の関数の実行と出力までで終わっていますが、本当に最小値となっているか少し心配なときがあります。

その場合は最小値の近くでグラフを書いてみるとわかりやすいです。

#最小値確認のためのグラフ作成
x_lis=np.arange(1500,1700,10)
f_lis=f(x_lis)

plt.plot(x_lis, f_lis,'-')
plt.xlabel('x [kg/cycle]')
plt.ylabel('f(x) [$/y]')
plt.show()

2行目でグラフでプロットするx軸の値を作成しています。

x=1500～1700まで10刻みで作っています。なぜ1500～1700かというと、一度計算して収束値を確認したからですね。

計算結果の確認

特に入力ミス等がなければ以下のように結果が表示されます。


総コストが最小となる1バッチ当たりの生産量[kg/cycle]: [1624.98701268]
総コスト最小値[$/y]: [516076.94519918]
総コストが最小となる場合の1サイクルにかかる時間[h/cycle]: [10.92365671]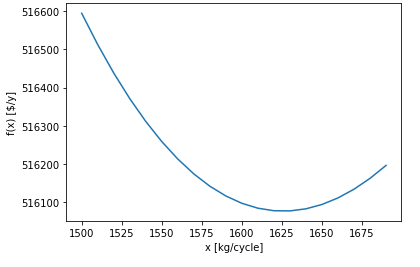

総コストが最小値になっているか確認するためにグラフを作成したところ、ちゃんと1625kg/cycleで最小値になっていますね。

全体のコードを下に載せておきます。

#モジュールインポート
import numpy as np
import matplotlib.pyplot as plt

#前提条件
cop=20  #運転期間のコスト[$/h]
cpp=15  #準備期間のコスト[$/h]
P=1000000  #年間生産量[kg/y]
raw=260000  #原材料費とその他諸経費[$/y]

#目的関数
def f(x):
    opcost=cop*1.5*x**0.25+cpp*1.4  #(5)式
    return opcost*P/x+340*x**0.8+raw

#偏微分と勾配の計算
def numerical_diff(f, x, i):
    h=1e-4
    h_vec=np.zeros_like(x)
    h_vec[i]=h
    return (f(x+h_vec)-f(x-h_vec))/(2*h)  #数値微分

def numerical_gradient(f, x):
    grad=np.zeros_like(x)
    for i, _ in enumerate(x):
        grad[i]=numerical_diff(f, x, i)
    return grad

#最急降下法
def gradient_descent(f, initial_position, learning_rate=0.1, steps=1000):
    x=initial_position
    for _ in range(steps):
        grad=numerical_gradient(f, x)
        x -= learning_rate * grad  #(2)式
    return x

#最急降下法の実行と出力
def main():
    min_pos = gradient_descent(f,[1000])  #最急降下法の実行
    CTmin=f(min_pos)  #(8)式
    tmin=1.5*min_pos**0.25+1.4  #(3)式
    print('総コストが最小となる1バッチ当たりの生産量[kg/cycle]: {0}'.format(min_pos))
    print('総コスト最小値[$/y]: {0}'.format(CTmin))
    print('総コストが最小となる場合の1サイクルにかかる時間[h/cycle]: {0}'.format(tmin))
main()  #関数の実行

#最小値確認のためのグラフ作成
x_lis=np.arange(1500,1700,10)
f_lis=f(x_lis)

plt.plot(x_lis, f_lis,'-')
plt.xlabel('x [kg/cycle]')
plt.ylabel('f(x) [$/y]')
plt.show()

まとめ

回分操作コスト計算を例にPythonで非線形最小二乗法の1つである最急降下法について計算しました。

比較的簡単な非線形関数であれば最急降下法で最小値を算出できます。複雑な関数なら別の手法を試した方がよいかもしれません。