概要
ラボスケールで開発してきた製品を量産化するために、反応器・反応槽を実機スケールへとスケールアップするのは化学工学エンジニアの代表的な仕事の1つと言えるでしょう。
スケールアップ後の実機寸法や撹拌条件をどのように決定すべきか、という課題は扱う系の特性によって変化します。
ただ、過去の知見から、スケールアップが成功しやすい指標がある程度体系化されています。
本記事では撹拌槽のスケールアップ指標についていくつかまとめました。
装置寸法のスケールアップ
幾何学的相似のスケールアップ
装置寸法のスケールアップで最も基本的でよく実施される手法が幾何学的相似のスケールアップです。
幾何学的相似とは撹拌槽や撹拌翼の寸法に一定の倍率をかけてスケールアップする手法です。
例えば、槽径Dを10倍にするスケールアップを実施するなら、翼径d、液高さHなども10倍の寸法に設定します。
以下に10倍スケールアップ時の寸法比較を示しました。
| 単位 | スケールアップ前 | スケールアップ後 (10倍) | |
| 槽径 | m | D | 10D |
| 翼径 | m | d | 10d |
| 液高さ | m | H | 10H |
| 伝熱面積 | m2 | ∝D2 | ∝100D2 |
| 液体積 | m3 | ∝D3 | ∝1000D3 |
単位液量当たりの 伝熱面積 | m2/m3 | ∝1/D | ∝1/(10D) |
一般に問題視されているのが、単位液量当たりの伝熱面積です。
10倍のスケールアップ時は単位液量当たりの伝熱面積がスケールアップ前の1/10となってしまい、伝熱能力不足となる可能性が高いです。
この問題を改善するために伝熱コイルを設置し伝熱面積を増加させる等の方法が考えられます。
詳しくは以下の記事で解説しています。
-

【撹拌槽伝熱】総括伝熱係数U・伝熱面積A・温度差ΔTそれぞれの改善手法を徹底解説
この記事では撹拌槽の伝熱能力についての考え方や計算方法、どのようにすれば伝熱性能を改善させることができるのか、について解説しています。
続きを見る
H/Dを大きくするスケールアップ
伝熱能力の確保が重要な系で、液高さH/槽径Dの比を大きくするスケールアップが実施されることがあります。
幾何学相似でスケールアップすると単位液量当たりの伝熱面積が減少します。この伝面減少をカバーするためにH/Dを大きくし、縦長の撹拌槽にするということです。
H/Dが大きくなると槽内の上下方向の混合性能が悪くなります。
混合性能悪化を抑制するために、
- 小型翼を複数設置し、多段翼とする。
- 大型翼を設置する。
- 回転数を増加する。
以上のような対応を実施することが多いです。
翼径dを大きくするスケールアップ
高分子などの非ニュートン流体を扱う場合に、翼径dを大きくしてスケールアップすることがあります。
非ニュートン流体の中でも、特にShear-thinning流体は撹拌翼によるせん断で粘度が変化します。
撹拌翼の近傍はせん断力が強いため粘度が小さくなり混合性が良いです。しかし翼から離れるにしたがって、せん断力が弱くなり粘度が高くなるため混合性が悪くなります。
この影響はスケールが大きくなるにつれてより顕著になります。
そこで、スケールアップ後の翼径dを大きくすることで翼のせん断が大きい領域を増やし、混合性を改善することができます。
特に小型翼は翼径を大きくする余地があるので、検討することをオススメします。
その他に、撹拌翼の種類自体を小型翼から大型翼に変更する方法も有効です。
回転数・翼径のスケールアップ
各スケールアップ手法で撹拌回転数と翼径がどのような関係になるか比較しました。
添え字の1をスケールアップ前、2をスケールアップ後と記載しています。
また前提条件として、スケールアップ前後の液物性は同一、乱流条件下で動力数Npは一定とします。
撹拌レイノルズ数一定のスケールアップ
撹拌レイノルズ数Reを一定としてスケールアップすると、
$$Re_{1}=Re_{2}・・・(1)$$
$$\frac{ρn_{1}{d_{1}}^{2}}{μ}=\frac{ρn_{2}{d_{2}}^{2}}{μ}・・・(2)$$
(1)、(2)式が成り立ちます。(2)式から、
$$\frac{n_{2}}{n_{1}}=(\frac{d_{1}}{d_{2}})^{2}・・・(3)$$
スケールアップ後の回転数n2は(3)式となります。
また、乱流条件下ではスケールアップ前後のNpは一定となりますから、
$$\frac{P_{1}}{ρ{n_{1}}^{3}{d_{1}}^{5}}=\frac{P_{2}}{ρ{n_{2}}^{3}{d_{2}}^{5}}・・・(4)$$
(4)式が成立します。(3)式を代入して整理すると、
$$\frac{P_{2}}{P_{1}}=\frac{d_{1}}{d_{2}}・・・(5)$$
となります。
撹拌レイノルズ数一定のスケールアップは槽内の流動状態が相似となります。
しかしスケールアップ後の回転数が小さくなり過ぎ混合不足となる可能性が高いため、実際にこの手法を使用したことはありません。
実務ではスケールアップ後の撹拌レイノルズ数は大きくなるような手法を使用することが多いです。
フルード数一定のスケールアップ
フルード数Frを一定としてスケールアップすると、
$$Fr_{1}=Fr_{2}・・・(6)$$
$$\frac{{n_{1}}^{2}d_{1}}{g}=\frac{{n_{2}}^{2}d_{2}}{g}・・・(7)$$
(6)、(7)式が成り立ちます。(7)式から、
$$\frac{n_{2}}{n_{1}}=(\frac{d_{1}}{d_{2}})^{1/2}・・・(8)$$
スケールアップ後の回転数n2は(8)式となります。
また、動力に関しては(8)式に(4)式を代入し整理すると、
$$\frac{P_{2}}{P_{1}}=(\frac{d_{1}}{d_{2}})^{-7/2}・・・(9)$$
となります。
フルード数一定条件ではバッフルが設置されていない場合に液面に生じる渦流が相似となります。
気液撹拌で気液界面からガス吸収を行なう場合など、液面の条件が重要な場合にこの手法が使用されることがあります。
Pv一定のスケールアップ
単位体積(液量)当たりの所要動力Pvを一定としてスケールアップすると、
$$\frac{P_{1}}{V_{1}}=\frac{P_{2}}{V_{2}}・・・(10)$$
(10)式が成り立ちます。
ここで、幾何学的相似条件のスケールアップだと仮定すると、
$$V∝d^{3}・・・(11)$$
(11)式とみなすことができます。
したがって、スケールアップ前後の動力の比は、
$$\frac{P_{2}}{P_{1}}=(\frac{d_{1}}{d_{2}})^{-3}・・・(12)$$
となります。
また、スケールアップ前後の回転数の比は、(12)式に(4)式を代入して整理すると、
$$\frac{n_{2}}{n_{1}}=(\frac{d_{1}}{d_{2}})^{2/3}・・・(13)$$
となります。
Pv一定のスケールアップは最も使用頻度の高い手法です。
ただし、スケールアップ後の混合時間が悪化するため、撹拌反応槽の設計には注意が必要です。
撹拌による混合速度に対して反応速度が十分に遅い場合は、多少混合時間が悪化しても影響はないでしょう。
ただし混合速度に対して反応速度がそれなりに速い場合は、スケールアップ後の反応率や転化率が悪くなることがあります。この場合は他の手法でスケールアップする方が良いでしょう。
翼端速度一定のスケールアップ
翼端速度を一定としてスケールアップすると、
$$πn_{1}d_{1}=πn_{2}d_{2}・・・(14)$$
(14)式が成り立ちます。したがって、
$$\frac{n_{2}}{n_{1}}=\frac{d_{1}}{d_{2}}・・・(15)$$
スケールアップ後の回転数n2は(15)式となります。
また、動力に関しては(15)式に(4)式を代入し整理すると、
$$\frac{P_{2}}{P_{1}}=(\frac{d_{1}}{d_{2}})^{-2}・・・(16)$$
となります。
Pv一定でスケールアップすると、スケールアップ後は翼端速度が大きくなるため翼によるせん断力が大きくなります。
晶析系や液液分散系など、翼のせん断力が重要となる場合には翼端速度を一定とすることが考えられます。
ただ、翼端速度一定としても粒子径分布が一定になるとは限らないので、この手法にどこまで価値があるか個人的には疑問です。
回転数一定のスケールアップ
回転数を一定としてスケールアップすると、
$$n_{1}=n_{2}・・・(17)$$
(17)式が成り立ちます。したがって、
また、動力に関しては(17)式に(4)式を代入し整理すると、
$$\frac{P_{2}}{P_{1}}=(\frac{d_{1}}{d_{2}})^{-5}・・・(18)$$
となります。
回転数一定のスケールアップでは無次元混合時間の関係から、混合時間が一定となることがわかります。
反応系で撹拌速度に対して反応速度が速い系では、混合時間一定でのスケールアップが求められることがあります。
また、回転数一定のスケールアップではスケールアップ後のPvが増大し、撹拌機サイズが大きくなってしまうことがデメリットとして挙げられます。
しかし、これはスケールアップ倍率によってどの程度のPv増大となるかが大きく変わってきます。
スケールアップ倍率が2倍のときはPvは倍、10倍のときは倍程度です。
したがって、スケールアップ倍率が大きいときは非現実的なPv増加となりますが、倍率が小さいときはそれなりに許容できる増加量と言えるでしょう。
スケールアップ時のPvの比較
各指標でのスケールアップにおいて、スケール比V2/V1が変化した場合のPv比(Pv)2/(Pv)1を比較したグラフを以下に示します。
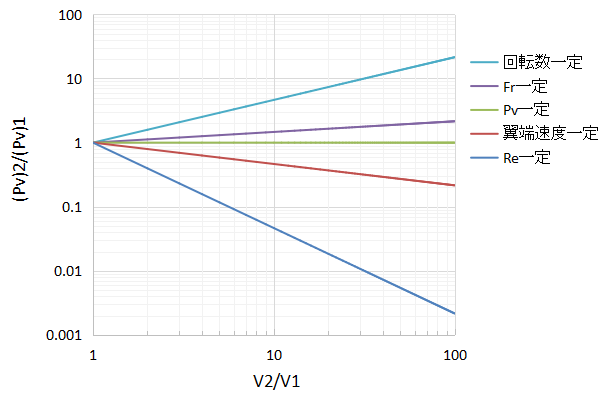
全体的な傾向として、横軸のスケール比が大きくなるにつれてPv比も大きく変化しています。
したがって、一気に大きい倍率でスケールアップしようとするほど難易度が高いことを示しています。
逆に小さい倍率のスケールアップではそれほどPv比の変化が大きくないため難易度が低いと言えます。
特に近年では実機スケールでも、少量多品種の倍率が小さいスケールアップが増えていることから、以前ほどPv一定のスケールアップに拘らなくてよいかもしれません。
おわりに
撹拌槽のスケールアップ指標についてまとめました。
一般的には装置寸法を幾何学相似とし、Pv一定でスケールアップすることが多いですが、例外もあります。
製品の要求スペックが細かくなるほど、Pv一定では対処しきれないことも増えてくるでしょう。どのような指標が有効かその都度検討する必要があります。
