概要
最小二乗法はあるデータとモデルによる計算値との差の二乗和が最小になるようモデルのパラメータを決定する手法です。
化学工学は化学実験や化学プラントで起こる現象を数式化して計算する学問と言ってもよいですが、残念ながらこの世で起こる全ての現象を体系化できているわけではありません。
特に新しく合成した化合物や製品がどのような現象を起こすかは予測が非常に難しいです。
そこで予測したい現象があれば実験をしてデータを取り、そのデータを数式化することで起こりえる現象を予測できるようになります。
この実験データを数式化することをデータ相関といい、データ相関手法の中でも最もよく使用されるモデルが最小二乗法です。
本記事では化学工学でよく線形相関されることが多いアレニウスプロットを例に線形最小二乗法を解説しています。
原理
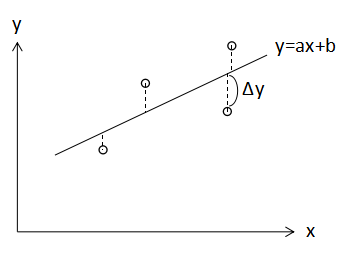
上の図のように線型的な相関がありそうなデータに対して、y=ax+bで表される近似直線を引くことを考えます。
任意の点(xi,yi)と近似直線との差Δyは
$$Δy=y_{i}-(ax_{i}+b)・・・(1)$$
となります。Δyがなるべく小さい方がデータ点と近似直線の値が近く、精度が良いことになります。
理想的には全てのデータ点のΔyがなるべくゼロに近い値になるとより精度が良いので、Δyの和をsとすると
$$s=\sum_{n=1}^{n}Δy=\sum_{n=1}^{n}y_{i}-(ax_{i}+b)・・・(2)$$
(2)式のsがゼロに近いとなることが望ましいです。
ただし、このままではSの最小値の評価が正しくできません。Δyは正負両方の値を取るため、データによっては正負のΔyが打ち消し合って誤差が大きいにも関わらずSの値がゼロに近づくことがあります。
そこでこのΔyの符号の影響をなくすためにΔyを2乗して和を求めます。
$$S=\sum_{n=1}^{n}(Δy)^{2}=\sum_{n=1}^{n}(y_{i}-(ax_{i}+b))^{2}・・・(3)$$
(3)式のSが最小値になるように定数a,bの値を決定することで精度の良い近似直線を引くことができます。この手法を線形の最小二乗法といいます。
また、(3)式の定数a,bは(3)式を偏微分することで解析的に算出することができます。
しかし表計算ソフトを使用すれば偏微分することなく簡単に最小二乗法を行なうことができるので、この記事では偏微分の説明は割愛します。
表計算ソフト計算例
アレニウスプロット
アレニウスプロットは化学の反応速度に関する関係式のことです。
反応速度定数kは、
$$k=A{\rm{exp}}(-\frac{E}{RT})・・・(4)$$
k:反応速度定数[m3/(mol・s)]、A:頻度因子[m3/(mol・s)]、E:活性化エネルギー[J/mol]
R:気体定数[J/(mol・K)]、T:温度[K]
(4)式で表されます。ちなみに反応速度定数の単位は反応の次数によって異なります。今回は2次反応をモデルとしています。
(4)式を両辺対数を取ると、
$${\rm{ln}}k={\rm{ln}}A-\frac{E}{R}\frac{1}{T}・・・(5)$$
(5)式となります。この(5)式を縦軸lnk、横軸1/Tとしてプロットすると直線になります。これをアレニウスプロットといいます。
温度を含む関数は非線形になりやすいのですが、式変形のみで線形プロットできる点が非常に優れています。
今回は以下の表に示すデータから活性化エネルギーEと頻度因子Aを算出してみましょう。
| T[K] | k[m3/(mol・s)] |
| 698.2 | 5.088E-4 |
| 740.2 | 1.506E-3 |
| 818.2 | 7.770E-3 |
| 887.2 | 2.678E-2 |
線形最小二乗法
ソルバー機能
今回紹介する中で最も最小二乗法っぽい手法がソルバー機能を使うものです。
(5)式を左辺-右辺の形にして二乗和をもとめ、ソルバーで二乗和が最小値となるようにE、Aの値を決定します。

上図にソルバー機能を使う前の入力値を示します。
A2セル、B2セルにはEとlnAの初期値を入力しています。ここではとりあえず両方100にします。
E2~E5セルに問題で与えられている温度Tを入力し、F2~F5セルに1/Tの値を計算させます。
同様にG2~G5セルに反応速度定数kを入力し、H2~H5セルにlnkの値を計算させます。
I2~I5セルに(5)式の左辺-右辺の二乗を計算して入力します。
最後にI6セルにI2~I5の和を計算して入力します。これでソルバーの準備は完了です。
次にExcel等の表計算ソフトのソルバー機能を使用します。
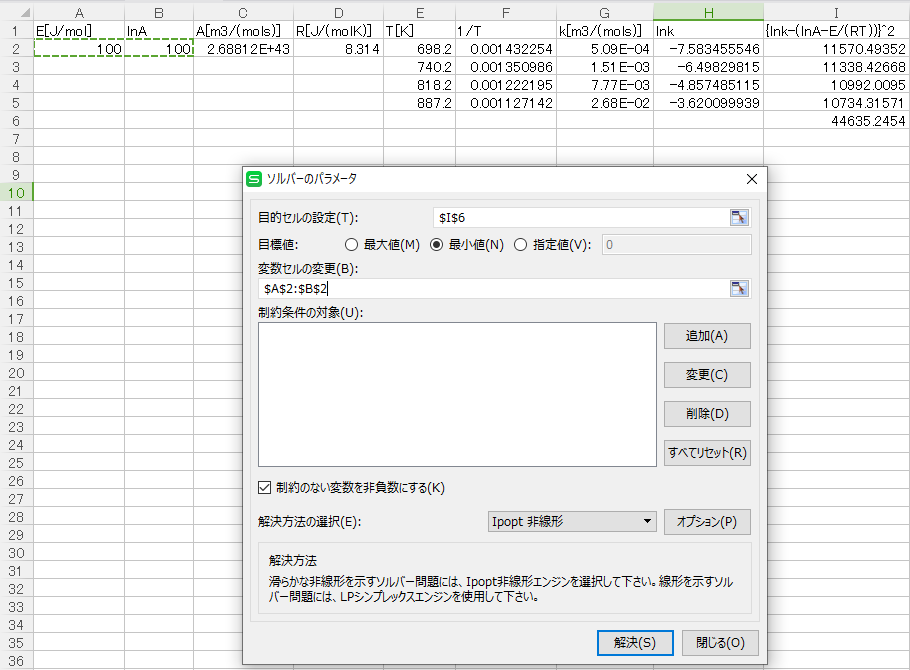
目的セルの設定は最小値を計算する関数を指定します。今回はI6セルの二乗和なので、I6セルを選択します。
目標値は最小値です。
変数セルの変更は、最小二乗法により決定するパラメータを指定します。今回はEとlnAですのでA2セルとB2セルを複数選択します。
これで右下の解決ボタンをクリックすればI6セルを最小化するように計算してくれます。

ソルバーの結果が上図になります。活性化エネルギーEは10,7670J/mol、lnAは10.977となりました。
頻度因子AはB2セルから58535m3/(mol・s)となりました。
今回は線形のソルバー計算なので収束しないことはないと思いますが、もし収束しないことがあればソルバー機能の設定を適宜変更することで改善する場合があります。
グラフの近似直線機能
視覚的に最もわかりやすい方法です。
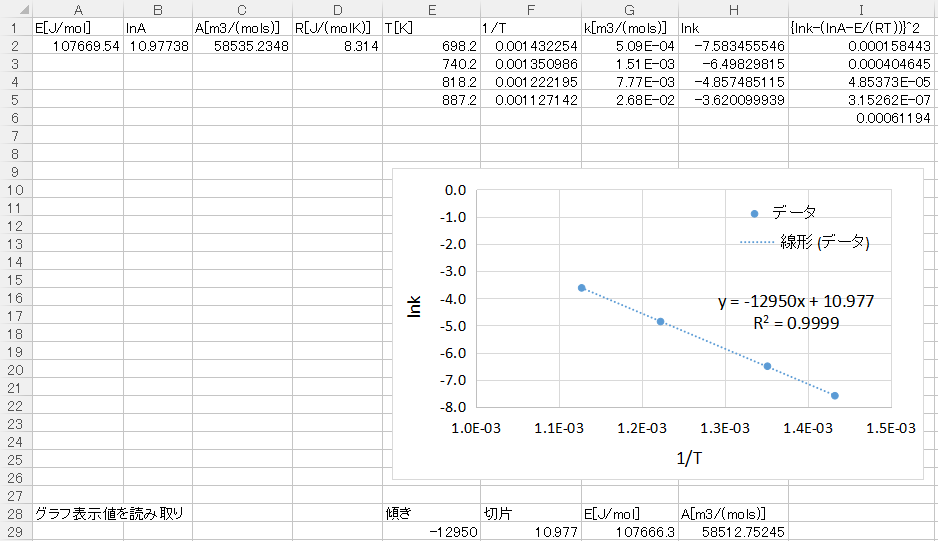
上図に示すように縦軸にH2~H5セルのlnk、横軸にF2~F5セルの1/Tをプロットしたグラフを作成し、グラフの直線近似機能を使用します。
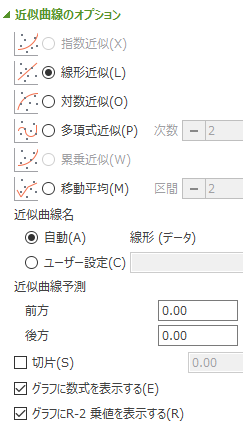
線形近似を選択し、下の方にある"グラフに数式を表示する"、"グラフにR-2乗値を表示する"にチェックを入れます。
そうするとグラフ上に近似直線の式が表示されるようになるため、この値からEとAの値を算出することができます。
グラフと(5)式から、
$$-12970=-\frac{E}{R}$$
$$10.977={\rm{ln}}k$$
となりますから、活性化エネルギーEは10,7666J/mol、頻度因子Aは58513m3/(mol・s)となりソルバー機能で求めた結果とほぼ同じになりました。
グラフでデータ点と線形プロットにどの程度のバラつきがあるかを視覚的に確認でき、R-2乗値でも定量的に確認できる点がこの手法のメリットです。
デメリットはグラフ上に表示された傾きと切片を手入力しなければならない点です。プロットするデータが何回も変わる場合は面倒です。
傾き・切片を算出する関数
前述したようにプロットするデータが変わりうる場合は、SLOPE関数とINTERCEPT関数を使用することで自動的に傾きと切片の値を取得することができます。
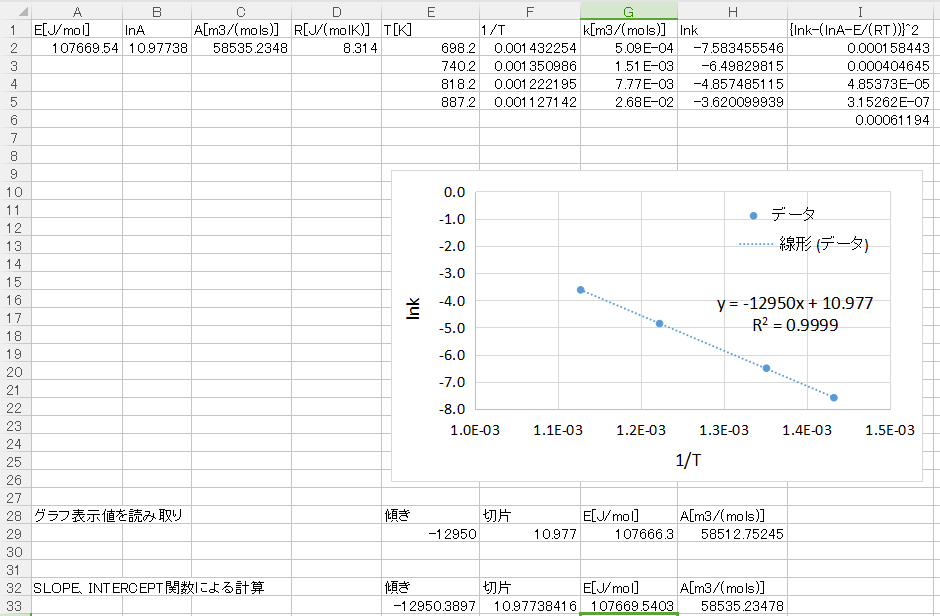
E33セルに=SLOPE(H2:H5,F2:F5)と入力することで縦軸lnk、横軸1/Tのデータをプロットした際の傾きを計算できます。
続いてF33セルに=INTERCEPT(H2:H5,F2:F5)と入力することで縦軸lnk、横軸1/Tのデータをプロットした際の切片を計算できます。
どちらもグラフ表示値とほぼ同じ結果となっているため、活性化エネルギーE、頻度因子Aもほぼ同じ値になっていますね。
ただし手法だけでは本当に適切な近似直線が引けているかわかりづらいため、グラフにプロットする手法と併用する方が良いでしょう。
まとめ
線形最小二乗法をアレニウスプロットを例に解説しました。
私は線形二乗法やアレニウスプロットを大学のときに習いましたが、未だに業務でも使用する重要な手法です。よく理解しておきましょう。
