概要
この記事では高圧ガス甲種機械の出題分野である、材料力学について解説します。
材料力学は毎年春(5月頃)に実施される検定試験、秋(11月頃)の国家試験の両方に出題されており、重要な分野です。
検定試験と国家試験のどちらも計算問題で出題されており、計算式をちゃんと覚えていないと正解できません。
ここでは検定試験の材料力学について解説します。
材料力学の出題分野
材料力学は学識の大問5問中の1問です。
本ブログ管理人のように化学工学専攻の人は、大学で材料力学を習うことはほとんどなく、会社の実務でも自分で計算することはないため難しく感じる分野だと思います。
問題構成としては、小問が3問前後で全て計算問題です。
計算式を覚えていないと1問も解けません。
ただし材料力学はその年の出題分野がある程度予測できるのが救いです。
過去数年の検定試験の出題内容については、
平成26年:熱応力
平成27年:薄肉円筒胴
平成28年:丸棒のねじれ
平成29年:熱応力
平成30年:薄肉円筒胴
令和元年:丸棒のねじれ
令和2年:熱応力
令和3年:薄肉円筒胴
令和4年:丸棒のねじれ
令和5年:熱応力
令和6年:薄肉円筒胴
このように熱応力・薄肉円筒胴・丸棒のねじれを3年でローテーションして出題されています。
この傾向通りであれば、次の試験で出題される分野を予想できますよね。
とはいえ念のため他の分野の勉強もしておいた方が良いでしょう。
以下に検定試験で過去に出題された内容をまとめました。
材料力学の基本概念
応力
垂直応力
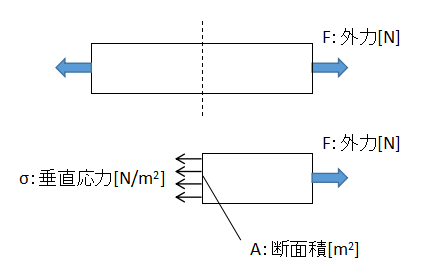
$$σ=\frac{F}{A}・・・(1)$$
σ:垂直応力[N/m2]、F:外力[N]、A:部材の断面積[m2]
材料力学の九九です。
試験では力のつり合いで式を立てるため、F=σAの形で使用することが多いでしょうか。
せん断応力
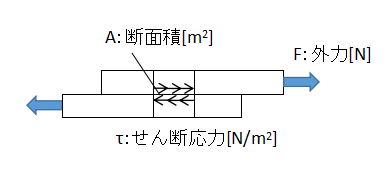
$$τ=\frac{F}{A}・・・(2)$$
τ:せん断応力[N/m2]、F:外力[N]、A:部材の断面積[m2]
せん断応力も似たような式で力のつり合いを表わすことができます。
ひずみ

上図に示すような部材を上に外力Fで引っ張ります。
このとき、縦方向はλだけ伸び、半径方向はδだけ縮みます。
このときの縦ひずみε、横ひずみε'は以下のように表せます。
(※材料圧縮の場合には符号が反対になるだけで式の形は変わりません。)
縦ひずみ
$$ε=\frac{λ}{l}・・・(3)$$
ε:縦ひずみ[-]、λ:伸び[m]、l:元の長さ[m]
横ひずみ
$$ε'=-\frac{δ}{d}・・・(4)$$
ε':横ひずみ[-]、δ:伸び[m]、d:元の直径[m]
ポアソン比
$$ν=\left|\frac{ε'}{ε}\right|=-\frac{ε'}{ε}・・・(5)$$
ν:ポアソン比[-]
ひずみそのものを計算する問題や、ひずみやポアソン比を与えて他のパラメータを計算する問題等、様々な形式で出題されています。
フックの法則
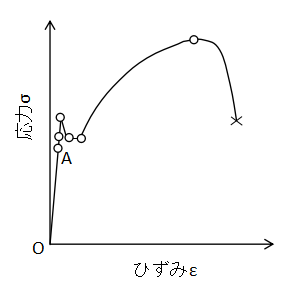
上図に応力-ひずみ線図の例を示します。
材料は点Oから点Aの区間までであれば、応力σとひずみεは比例関係にあります。
この区間OAで成り立つ法則をフックの法則といい、(6)式で表されます。
$$σ=Eε・・・(6)$$
σ:垂直応力[N/m2]、E:縦弾性係数[N/m2]、ε:横ひずみ[-]
せん断応力の場合には、
$$τ=Gγ・・・(7)$$
τ:せん断応力[N/m2]、G:横弾性係数[N/m2]、γ:せん断ひずみ[-]
(7)式となります。
3次元応力とひずみ
1次元の応力とひずみの計算は前述した(1)~(7)式で計算できます。
しかし検定試験では3次元の応力とひずみの計算が求められることがあります。
特に薄肉円筒胴の計算ではほぼ必ず3次元のひずみについて計算しますので覚えておきましょう。
主ひずみ
$$ε_{1}=\frac{1}{E}(σ_{1}-ν(σ_{2}+σ_{3}))・・・(8)$$
$$ε_{2}=\frac{1}{E}(σ_{2}-ν(σ_{3}+σ_{1}))・・・(9)$$
$$ε_{3}=\frac{1}{E}(σ_{3}-ν(σ_{1}+σ_{2}))・・・(10)$$
ε1,ε2,ε3:主ひずみ[-]、E:縦弾性係数[N/m2]
ν:ポアソン比[-]、σ:主応力[N/m2]
3次元の主ひずみは(8)~(10)式で表されます。
3つの式の形は同じなので、どれか1つを覚えておけば応用できるでしょう。
主応力
(8)~(10)式から主応力σ1,σ2,σ3を算出することができます。
$$σ_{1}=\frac{E}{(1+ν)(1-2ν)}((1-ν)ε_{1}+ν(ε_{2}+ε_{3}))・・・(11)$$
$$σ_{2}=\frac{E}{(1+ν)(1-2ν)}((1-ν)ε_{2}+ν(ε_{3}+ε_{1}))・・・(12)$$
$$σ_{3}=\frac{E}{(1+ν)(1-2ν)}((1-ν)ε_{3}+ν(ε_{1}+ε_{2}))・・・(13)$$
(8)~(10)式を覚えておけば(11)~(13)式は導出できますので覚える必要はないと思います。
主せん断応力
主せん断応力τは(14)~(16)式で表されます。
$$τ_{1}=±\frac{1}{2}(σ_{2}-σ_{3})・・・(14)$$
$$τ_{2}=±\frac{1}{2}(σ_{3}-σ_{1})・・・(15)$$
$$τ_{3}=±\frac{1}{2}(σ_{1}-σ_{2})・・・(16)$$
また、試験では特に最大主せん断応力τmaxを問われることがあります。
最大主せん断応力τmaxは主応力のうちの最大応力と最小応力の差を1/2で割ったものになります。
$$τ_{max}=±\frac{1}{2}(σ_{max}-σ_{min})・・・(17)$$
熱応力
ローテーションで出題される分野の1つです。
基本的に丸棒の熱応力・熱膨張を計算することが多いですが、丸棒の形状は出題年によって様々です。
過去に出題された部材形状がそのまま出題されることはないでしょう。
したがって過去問を丸暗記するだけでは解くことはできず、理論を理解してその場で式を立てる必要があります。
部材の伸び(縮み)・熱応力
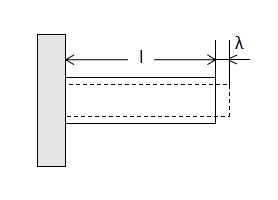
部材は温度変化によって伸び縮みします。
部材の自由な熱膨張(熱収縮)による伸び(縮み)をλとすると、
$$λ=αΔTl・・・(18)$$
λ:部材の伸び(縮み)[m]、α:線膨張係数[K-1]、l:部材の元の長さ[m]
(18)式で表すことができます。
また、部材が拘束された状態で温度変化が起きると、部材の自由な熱膨張(熱収縮)が妨げられて(19)式の熱応力σ[N/m2]が発生します。
$$σ=-αEΔT・・・(19)$$
部材拘束時の計算
熱応力の問題では、部材の伸び(縮み)λについて式を立てて計算することが多いです。
部材が拘束された状態ではλ=0として計算します。
ポイントとしては、λは熱膨張(熱収縮)による伸び(縮み)と、生じた熱応力による伸縮の両方を考慮する必要があります。
熱膨張(熱収縮)は(18)式、熱応力伸縮は(3),(6)式を使用します。
一般形としては、
$$λ=αΔTl+\frac{σl}{E}=0・・・(20)$$
(20)式のような形となります。
薄肉円筒胴・球形胴
円筒胴・球形胴系の分野は大きく分けて4つあります。
・薄肉円筒胴
・薄肉球形胴
・厚肉円筒胴
・厚肉球形胴
薄肉胴の方が簡略化した計算式なので簡単ですが、厚肉胴はかなり難しいです。
ただ、厚肉胴は5月の検定試験はもとより11月の国家試験でもほとんど出題されていません。
検定試験では薄肉円筒胴、薄肉球形胴の2つを勉強しておけばまず大丈夫でしょう。
薄肉円筒胴
薄肉円筒胴が受ける内圧pについて、円周方向、軸方向、半径方向それぞれの応力を求めます。
円周応力
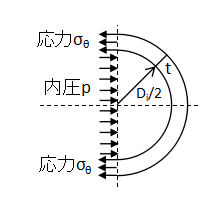
上図のような円筒胴を輪切りにした断面で、円筒胴が受ける内圧pについて考えます。
厳密には各円周部に内圧p[N/m2]が作用していますが、上下方向については対称性によって相殺されています。
したがって、水平方向にのみ圧力pが作用しているとみなすことができます。
内圧pが作用する面積は、円筒の直径Di×円筒の軸方向長さLとなります。
また、この内圧pによって生じる円周応力σθ[N/m2]は円筒の薄肉部に生じます。
本来なら円周応力σθは円筒の厚み方向で値が変化しますが、薄肉円筒胴の仮定では円周応力σθは厚み方向によらず一定値として考えることができます。
よって、内圧pと円周応力σθの力のつり合いについて式を立てると、
$$p・D_{i}L=σ_{θ}・2tL$$
$$σ_{θ}=\frac{pD_{i}}{2t}・・・(21)$$
Di:円筒胴内径[m]、t:円筒胴厚み[m]
円周応力σθは(21)式で表せます。
式の形は簡単なので丸暗記しても良いと思いますが、分母の係数2が他の式と間違えやすいので注意です。
軸応力
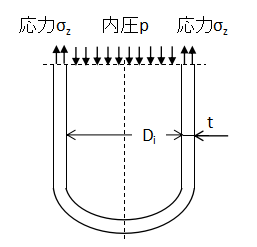
上図に円筒胴の縦断面図を示します。
同様に内圧Pと円筒胴の厚みにかかる軸応力σzについて力のつり合いから式を立てると、
$$p・\frac{πD_{i}^{2}}{4}=σ_{z}・πD_{i}t$$
$$σ_{z}=\frac{pD_{i}}{4t}・・・(22)$$
Di:円筒胴内径[m]、t:円筒胴厚み[m]
軸応力σzは(22)式で表せます。
軸応力σzは円周応力σθよりも小さく、σz=σθ/2となることを覚えておきましょう。
半径応力
半径応力σrはσθ、σzと比較してはるかに小さいため、
$$σ_{r}=0・・・(23)$$
として扱います。
最大主応力
設計上は円周応力σθ、軸応力σz、半径応力σrのうち、最も値が高くなる成分の応力に耐えられるよう肉厚tを決めます。
前述した内容から、
$$σ_{max}=σ_{θ}・・・(24)$$
円周応力σθが最大主応力σmaxとなります。
検定試験でも、最大主応力σmaxが与えられて計算する問題が出題されていますので覚えておきましょう。
最大せん断応力
最大せん断応力τmaxは(16)式から、最大主応力σθと最小主応力σrを使用して表します。
$$τ_{max}=\frac{1}{2}(σ_{θ}-σ_{r})=\frac{1}{2}σ_{θ}・・・(25)$$
最大主応力σmaxの1/2になることを覚えておきましょう。
円周方向ひずみ
円周方向ひずみεθは、
$$ε_{θ}=\frac{π(D_{i}+ΔD)-πD_{i}}{πD_{i}}=\frac{ΔD}{D_{i}}・・・(26)$$
(26)式で表されます。
また、3次元のひずみ(8)式を薄肉円筒胴の円周応力σθ、軸応力σz、半径応力σrに当てはめると、
$$ε_{θ}=\frac{1}{E}(σ_{θ}-ν(σ_{z}+σ_{r}))=\frac{1}{E}(σ_{θ}-νσ_{z})・・・(27)$$
(27)式となります。
この(27)式も出題されやすいので覚えておきましょう。
軸方向ひずみ
軸方向ひずみεzも同様に軸応力σzを主応力として3次元のひずみ(8)式に当てはめると、
$$ε_{z}=\frac{1}{E}(σ_{z}-ν(σ_{r}+σ_{θ}))=\frac{1}{E}(σ_{z}-νσ_{θ})・・・(28)$$
となります。
薄肉球形胴
前述したものは容器の円筒部についてでしたが、こちらは容器の球形の鏡部が受ける内圧pについて計算します。
内圧pが作用する場合に生じる主応力は、直交する2方向の接線応力σθと半径応力σrとなります。
球形で対称形状なので、軸方向の応力σzは接線応力σθとみなせます。
接線応力
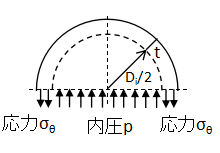
上図の半球断面で球形胴が受ける力について考えます。
同様に内圧pと接線応力σθの力のつり合いについて式を立てると、
$$p・\frac{πD_{i}^{2}}{4}=σ_{θ}・πD_{i}t$$
$$σ_{θ}=\frac{pD_{i}}{4t}・・・(29)$$
Di:球形胴内径[m]、t:球形胴厚み[m]
接線応力σθは(29)式で表せます。
円筒胴と比較して、分母の係数が4になっています。
間違えやすいので式の導出から理解した方が覚えやすいです。
半径応力
半径応力σrは薄肉円筒胴の場合と同様に、
$$σ_{r}=0・・・(30)$$
として扱います。
最大主応力
最大主応力σmaxは、
$$σ_{max}=σ_{θ}・・・(31)$$
円周応力σθが最大主応力σmaxとなります。
最大せん断応力
最大せん断応力τmaxは、
$$τ_{max}=\frac{1}{2}(σ_{θ}-σ_{r})=\frac{1}{2}σ_{θ}・・・(32)$$
となります。
円周方向ひずみ
円周方向ひずみεθも同様に、
$$ε_{θ}=\frac{ΔD}{D_{i}}・・・(33)$$
(33)式で表されます。
3次元のひずみ(8)式を薄肉円筒胴の円周応力σθ、半径応力σrに当てはめると、
$$ε_{θ}=\frac{1}{E}(σ_{θ}-ν(σ_{θ}+σ_{r}))=\frac{1-ν}{E}σ_{θ}・・・(34)$$
(34)式となります。
丸棒のねじれ
丸棒もしくは中空丸棒のねじれが出題されています。
問題のパターンはほとんど決まっているので、計算式を覚えるか導出できるようにしておくことが重要です。
いくつかの参考書を見ましたが、丸棒のねじれについてしっくりとくる導出を見つけられなかったので、ブログ管理人はこの分野は式の丸暗記で乗り切りました。
最大せん断応力
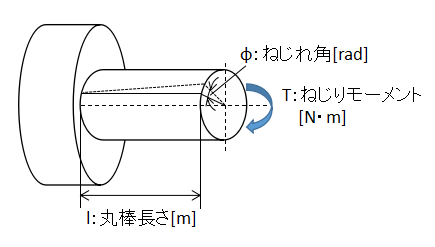
丸棒の外面に生じる最大せん断応力τmax[N/m2]は、
$$τ_{max}=\frac{16T}{πd^{3}}・・・(35)$$
T:ねじりモーメント[N・m]、d:丸棒直径[m]
(35)式で表されます。
また、中空丸棒の外面に生じる最大せん断応力τmax[N/m2]は、
$$τ_{max}=\frac{16d_{2}T}{π(d_{2}^{4}-d_{1}^{4})}・・・(36)$$
T:ねじりモーメント[N・m]、d1:内径[m]、d2:外径[m]
(36)式で表されます。
端面のねじれ角
丸棒端面のねじれ角Φ[rad]は、
$$Φ=\frac{32lT}{πd^{4}G}・・・(37)$$
l:丸棒の長さ[m]、G:横弾性係数[Pa]
(37)式で表されます。
また、中空丸棒端面のねじれ角Φ[rad]は、
$$Φ=\frac{32lT}{π(d_{2}^{4}-d_{1}^{4})G}・・・(38)$$
(38)式で表されます。
(35)~(38)式を覚えていれば、丸棒のねじれの問題は解けるはずです。
まとめ
高圧ガス甲種機械の検定試験範囲である、材料力学についてまとめました。
過去の傾向から、3年ごとに熱応力・薄肉円筒胴・丸棒のねじれがローテーションして出題されているので、自分の受験する年がどれに当てはまるか確認しましょう。
ただし、他の分野が絶対に出題されないとは限らないので、念のため勉強しておくことをオススメします。
