【圧縮機・ポンプ】高圧ガス甲種機械：検定試験の出題分野を解説

概要

この記事では高圧ガス甲種機械の出題分野である、圧縮機・ポンプの分野について解説します。

圧縮機・ポンプの分野は毎年春(5月頃)に実施される検定試験、秋(11月頃)の国家試験の両方に出題されており、重要な分野です。

検定試験と国家試験ともに計算問題で出題されており、他の分野と比較して難易度が高めです。

しかし非常に実用的な分野でもあり、将来的に実務で携わる、あるいはすでに携わっているという人もいるでしょう。

ここでは検定試験の圧縮機・ポンプの分野について解説します。

圧縮機・ポンプの出題分野

圧縮機・ポンプは学識の大問5問中の1問です。

ただし、他の出題分野の応用的な内容でもあり難易度は高めです。

圧縮機は"気体の熱力学"、ポンプは"流体の流れ"の分野の応用となっています。

気体の熱力学と流体の流れの出題分野については以下の記事で解説しています。

【気体の熱力学】高圧ガス甲種機械：検定試験の出題分野を解説

この記事では高圧ガス甲種機械の出題分野である、気体の熱力学について解説します。
気体の熱力学は毎年春(5月頃)に実施される検定試験、11月の国家試験の両方に出題されており、重要な分野です。

続きを見る

【流体の流れ】高圧ガス甲種機械：検定試験の出題分野を解説

この記事では高圧ガス甲種機械の出題分野である、流体の流れについて解説します。他の大問と比較して、流体の流れは簡単なので確実に点を取りたいところです。

続きを見る

出題傾向としては、毎年圧縮機かポンプのどちらかについて出題されています。
(たまに圧縮機・ポンプ両方の内容が問われることもあります。)

ここ数年は、

平成26年：遠心圧縮機(ポリトロープ圧縮)

平成27年：往復圧縮機

平成28年：ポンプ

平成29年：ターボ形圧縮機・ポンプ

平成30年：ターボ形圧縮機(ポリトロープ圧縮)

令和元年：往復圧縮機

令和2年：往復ポンプ

令和3年：ポンプ(NPSH)

このような出題傾向です。出題に偏りがあるわけではなさそうです。

どちらかにヤマを張るのは個人の自由ですが、内容としてはどちらの分野も実用的なので、ちゃんと勉強して知っておいた方が今後のためにはなると思います。

往復圧縮機

往復圧縮機の問題では、

・等温圧縮の仕事
・断熱圧縮の仕事

いずれかが出題される可能性が高いのでよく勉強しておきましょう。

往復圧縮機のサイクルと仕事の定義

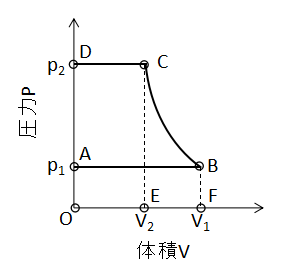
1段往復圧縮機のサイクルは上図のようなP-V線図で表されます。

ここでは、シリンダーに全く隙間のない理想的な圧縮機を考えます。

まずA→Bの過程で圧縮機に気体を取り込み、吸気口を閉じます。

次にB→Cの過程で取り込んだ空気を圧縮します。
圧縮は等温圧縮、断熱圧縮、その他の圧縮など場合によって様々です。

次にC→Dの過程で圧縮した気体を吐出口から吐出します。

最後にD→Aの過程で吐出口を閉じ、吸気口を開くことで圧力が吸気側と同じ圧力まで低下します。

この一連のサイクルが圧縮機のサイクルとなります。
このときの圧縮機がする仕事Wについて、気体が外から受ける仕事を正として表すと、

$$W=-吸込仕事(ABFO)+圧縮仕事(BCEF)+吐出仕事(CDOE)$$

となります。

それぞれの面積を差し引きすると、サイクルの仕事の面積はABCDとなります。

この面積ABCDについて、縦軸をV、横軸をPに軸を変更して表すと下図のようになります。

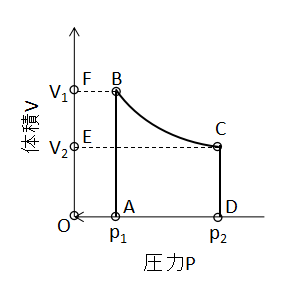
この図から、体積Vの関数について圧力p₁からp₂まで積分して求められる面積がABCDとなります。

したがって、圧縮機の仕事の定義式は(1)式となります。

$$W=\int_{p_{1}}^{p_{2}}Vdp・・・(1)$$

(1)式は等温圧縮、断熱圧縮における仕事の算出の基礎式となりますから必ず覚えておきましょう。

理論サイクルの仕事

等温圧縮の場合

等温圧縮の仕事W[J]は、圧縮機の仕事の定義式(1)式を積分することで算出できます。

$$W=\int_{p_{1}}^{p_{2}}Vdp=\int_{p_{1}}^{p_{2}}\frac{nRT_{1}}{p}dp$$

等温圧縮なのでTは定数とみなすことができ、圧力Pで積分できます。

$$W=nRT_{1}[{\rm{ln}}p]^{p_{2}}_{p_{1}}=nRT_{1}{\rm{ln}}(\frac{p_{2}}{p_{1}})・・・(2)$$

(2)式が等温圧縮の仕事Wとなります。

また、後々に理論圧縮動力を求めることを考えると、1mol当たりの仕事W_ad[J/mol]、1kg当たりの仕事w_ad[J/kg]で表した方が都合が良いです。

$$W_{ad}=RT_{1}{\rm{ln}}(\frac{p_{2}}{p_{1}})・・・(3)$$

$$w_{ad}=\frac{RT_{1}}{M}{\rm{ln}}(\frac{p_{2}}{p_{1}})・・・(4)$$

M：モル質量[kg/mol]

断熱圧縮の場合

断熱圧縮の仕事W[J]も同様に圧縮機の仕事の定義式(1)式を積分することで算出できます。

$$pV^{γ}=p_{1}V_{1}^{γ}・・・(5)$$

$$V=V_{1}(\frac{p_{1}}{p})^{\frac{1}{γ}}$$

断熱変化の関係式(5)式を変形して(1)式に代入します。

$$\begin{align}W&=\int_{p_{1}}^{p_{2}}V_{1}(\frac{p_{1}}{p})^{\frac{1}{γ}}dp\\&
=\frac{γ}{γ-1}p_{1}^{\frac{1}{γ}}V_{1}[p^{\frac{γ-1}{γ}}]^{p_{2}}_{p_{1}}=\frac{γ}{γ-1}p_{1}^{\frac{1}{γ}}V_{1}\Biggl(p_{2}^{\frac{γ-1}{γ}}-p_{1}^{\frac{γ-1}{γ}}\Biggr)\\&
=\frac{γ}{γ-1}p_{1}V_{1}\Biggl((\frac{p_{2}}{p_{1}})^{\frac{γ-1}{γ}}-1\Biggr)\\&=\frac{γ}{γ-1}nRT_{1}\Biggl((\frac{p_{2}}{p_{1}})^{\frac{γ-1}{γ}}-1\Biggr)・・・(6)\end{align}$$

最終的に(6)式が断熱圧縮の仕事Wとなります。

1mol当たりの仕事W_ad[J/mol]、1kg当たりの仕事w_ad[J/kg]は(6)式から、

$$W_{ad}=\frac{γ}{γ-1}RT_{1}\Biggl((\frac{p_{2}}{p_{1}})^{\frac{γ-1}{γ}}-1\Biggr)・・・(7)$$

$$w_{ad}=\frac{γ}{γ-1}\frac{RT_{1}}{M}\Biggl((\frac{p_{2}}{p_{1}})^{\frac{γ-1}{γ}}-1\Biggr)・・・(8)$$

(7),(8)式となります。

覚えることが難しければ、試験中に導出できるように理論を理解しておきましょう。

理論圧縮動力

理論圧縮動力P_th[W]は、理論サイクルの仕事にモル流量Q_m[mol/s]、もしくは質量流量q_m[kg/s]をかけた値となります。

等温圧縮の場合

(3),(4)式から、

$$P_{th}=Q_{m}W_{ad}=Q_{m}RT_{1}{\rm{ln}}(\frac{P_{2}}{P_{1}})・・・(9)$$

$$P_{th}=q_{m}w_{ad}=q_{m}\frac{RT_{1}}{M}{\rm{ln}}(\frac{P_{2}}{P_{1}})・・・(10)$$

となります。

断熱圧縮の場合

(7),(8)式から、

$$P_{th}=Q_{m}W_{ad}=Q_{m}\frac{γ}{γ-1}RT_{1}\Biggl((\frac{p_{2}}{p_{1}})^{\frac{γ-1}{γ}}-1\Biggr)・・・(11)$$

$$P_{th}=q_{m}w_{ad}=q_{m}\frac{γ}{γ-1}\frac{RT_{1}}{M}\Biggl((\frac{p_{2}}{p_{1}})^{\frac{γ-1}{γ}}-1\Biggr)・・・(12)$$

となります。

正味の軸動力

圧縮に必要な動力P[W]は、理論圧縮動力P_thと圧縮効率ηを使用して、

$$P=\frac{P_{th}}{η}・・・(13)$$

(13)式で表されます。

さらに、正味の軸動力P_shは機械損失P_mを考慮して、

$$P_{sh}=P+P_{m}・・・(14)$$

(14)式で表されます。

ポリトロープ変化

実際の圧縮機の状態変化は、等温変化と断熱変化の中間のような状態変化となっています。

このような状態変化をポリトロープ変化といいます。

とは言っても計算式が複雑化することはなく、断熱変化の関係式について、比熱容量の比γをポリトロープ指数nに置き換えて使用することができます。
(※モル数nのことではないので混同しないようにしましょう。)

ポリトロープ変化の仕事w_ad[J/kg]の計算式は(8)式をポリトロープ指数nに置き換えた(15)式となります。

$$w_{ad}=\frac{n}{n-1}\frac{RT_{1}}{M}\Biggl((\frac{p_{2}}{p_{1}})^{\frac{n-1}{n}}-1\Biggr)・・・(15)$$

また、ポリトロープヘッドH_pol[m]は(15)式を重力加速度gで割った(16)式となります。

$$H_{pol}=\frac{n}{n-1}\frac{RT_{1}}{Mg}\Biggl((\frac{p_{2}}{p_{1}})^{\frac{n-1}{n}}-1\Biggr)・・・(16)$$

往復ポンプ

往復ポンプの問題は、

・ポンプの全揚程
・ポンプの理論動力
・ポンプの軸動力

以上の3点が出題されることが多いです。よく勉強しておきましょう。

ポンプの全揚程

ポンプの全揚程Hは通常、流路に圧力損失があるものとして計算されます。

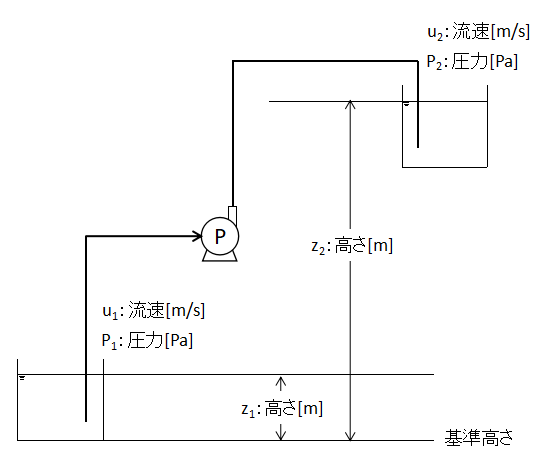
上図のような系におけるポンプの全揚程は、

$$H=\frac{u_{2}^{2}-u_{1}^{2}}{2g}+z_{2}-z_{1}+\frac{P_{2}-P_{1}}{ρg}+H_{f}・・・(17)$$

H：全揚程[m]、u₁,u₂：平均流速[m/s]、g：重力加速度[m/s²]
z₁,z₂：基準面からの高さ[m]、P₁,P₂：圧力[Pa]、H_f：損失水頭[m]

(17)式で表されます。

いわゆるベルヌーイの定理に損失水頭H_fを加えた式です。

詳しくは以下の記事で解説しています。

【ベルヌーイの定理】をわかりやすく解説：ポンプ揚程計算の基礎式

流体に関するエネルギー保存則のことを特にベルヌーイの定理といいます。ベルヌーイの定理が成り立つおかげで、エンジニアは流体を所定の高さまで持ち上げるのにどのくらいのエネルギーやポンプ性能が必要か計算できるわけです。

続きを見る

参考書によく載っているような大気開放されたタンク間での流体の送液について(17)式を簡単に表すと、

$$H=h_{a}+h_{fs}+h_{fd}+h_{o}・・・(18)$$

$$h_{a}=z_{2}-z_{1}・・・(19)$$

$$H_{f}=h_{fs}+h_{fd}・・・(20)$$

$$h_{o}=\frac{u_{2}^{2}-u_{1}^{2}}{2g}・・・(21)$$

$$\frac{P_{2}-P_{1}}{ρg}=0・・・(22)$$

H：全揚程[m]、h_a：実揚程[m]、h_fs：吸込み側摩擦損失水頭[m]
h_fd：吐出し側摩擦損失水頭[m]、h_o：残留速度水頭[m]

(18)式のようになります。

どちらのタンクも大気開放なので圧力差P₂-P₁=0となり、式が簡単になります。
また、吸込み側の流速u₁=0として扱うことが多いです。

(18)式は圧力差がある場合には使えないので、実務では(17)式がベースになります。

(18)式は正直使いにくいのですが、試験では(18)式の形で問われることが多いので念のため覚えておきましょう。

損失水頭

損失水頭H_fはさらに摩擦損失水頭と形状損失水頭に分けられます。

吸込み側摩擦損失水頭h_fsと吐出し側摩擦損失水頭h_fdのどちらも同じように計算できます。

$$h_{fs}=h_{f}+h_{l}・・・(23)$$

$$h_{fd}=h_{f}+h_{l}・・・(24)$$

なのでわざわざ吸込み側と吐出し側に分けて計算する必要性は全くないのですが、試験では(18)式で出題されることが多いので気を付けましょう。

摩擦損失水頭

摩擦損失水頭h_fは直管の圧力損失のことです。

乱流の場合は、ファニングの式で算出できます。

$$h_{f}=\frac{ΔP}{ρg}=4f\frac{u^{2}}{2g}\frac{L}{d}・・・(25)$$

ΔP：圧力損失[Pa]、f：摩擦係数[-]、ρ：流体密度[kg/m³]
u：流体の平均速度[m/s]、L：配管長さ[m]、d：配管直径[m]

詳しくは下の記事で解説しています。

【ファニングの式】を導出方法含めて解説：直管の圧力損失計算式

配管の圧力損失計算で使用される式をファニングの式といいます。もしファニングの式で圧力損失を考慮せずに実揚程だけでポンプの揚程を決めてしまうと、流体と配管との摩擦によりエネルギーが損失するため、目的の場所まで流体を送ることができなくなります。

続きを見る

層流の場合は、ハーゲン・ポアズイユの式で算出できます。

$$h_{f}=\frac{ΔP}{ρg}=\frac{32μLu}{ρgd^{2}}・・・(26)$$

ΔP：圧力損失[Pa]、μ：流体粘度[Pa・s]
u：流体の平均速度[m/s]、L：配管長さ[m]、d：配管直径[m]

詳しくは下の記事で解説しています。

【ハーゲン・ポアズイユの式】を解説：層流の圧力損失計算式

層流の配管流れにおける圧力損失と流速の関係式をハーゲン・ポアズイユの式といいます。本記事ではハーゲン・ポアズイユの式の導出について解説します。

続きを見る

形状損失水頭

形状損失水頭h_lは流路の形状や弁の種類によって、使用する式や係数が異なります。

全てを暗記するのは難しいので、実務での関わりがなさそうならある程度割り切って捨ててもよいかもしれません。

以下の記事で摩擦損失水頭h_fや形状損失水頭h_lについて詳しく解説しています。

配管流路【圧力損失】の計算方法を形状ごとに解説

流体が壁面との摩擦や流体同士の摩擦によってエネルギーを損失することを圧力損失といいます。この記事では実務で計算する頻度の多い配管流路の圧力損失について計算方法を紹介します。

続きを見る

理論動力

ポンプの理論動力は(27)式で表されます。

$$P_{th}=q_{m}gH=q_{V}ρgH・・・(27)$$

P_th：理論動力[W]、q_m：質量流量[kg/s]、q_V：体積流量[m³/s]
ρ：流体密度[kg/m³]、g：重力加速度[m/s²]、H：全揚程[m]

小問(1)で全揚程Hを計算して、小問(2),(3)で理論動力や軸動力を計算する問題が多いです。

軸動力

ポンプの軸動力は(28)式で表されます。

$$P_{s}=\frac{P_{th}}{η}・・・(28)$$

P_s：軸動力[W]、η：ポンプ効率[-]

ターボ形圧縮機・ポンプ

オイラーの式

ターボ形圧縮機やターボ形ポンプは羽根車の回転により流体にエネルギーを与えます。

そのため、羽根車の特性が流体へ与えるエネルギーやヘッドに大きく影響しており、その関係式をオイラーの式といいます。

下図に示すような羽根車の理論ヘッドH_thは(29)式で算出することができます。

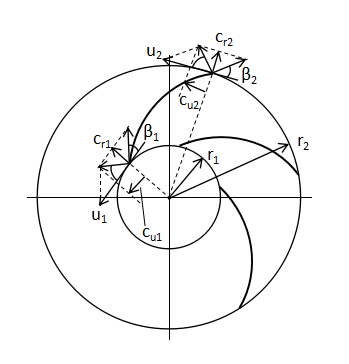
$$H_{th}=\frac{1}{g}(u_{2}c_{u2}-u_{1}c_{u1})・・・(29)$$

H_th：理論ヘッド[m]、g：重力加速度[m/s²]
r₁,r₂：羽根車の入口,出口の半径[m]
u₁,u₂：羽根車の入口,出口の円周速度[m/s]
c_u1,c_u2：羽根車の入口,出口における流れの円周方向速度[m/s]
β₁,β₂：羽根車の入口,出口における角度

(29)式は導出が複雑なため、実務で羽根車の設計に携わる人でもない限りは丸暗記した方が良いと思います。

加えて、普通は羽根車入口の流れの円周速度c_u1はゼロとなるので(29)式は

$$H_{th}=\frac{1}{g}u_{2}c_{u2}・・・(30)$$

(30)式のように簡略化できます。

ただし、(29),(30)式には求めることが難しいパラメータである羽根車入口・出口の流れの円周速度c_u1,c_u2が含まれています。

ターボ形圧縮機・ポンプを設計するうえでこのようなパラメータが含まれていると不便なので、羽根車の寸法や回転数等、設計者が決定できるパラメータに変形します。

羽根車出口の流れの円周速度c_u2は、

$$c_{u2}=u_{2}-\frac{c_{r2}}{tanβ_{2}}・・・(31)$$

c_r2：流れの半径方向速度[m/s]、β₂：羽根の出口部角度

(31)式で表されます。

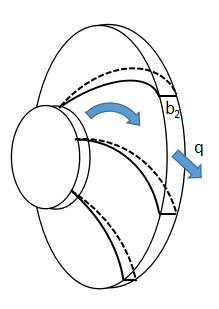
続いて上図は羽根車を斜めから見た模式図です。

羽根車出口の体積流量q[m³/s]は、羽根車出口幅をb₂とすると、

$$q=2πr_{2}b_{2}c_{r2}$$

上式で表され、変形すると(32)式となります。

$$c_{r2}=\frac{q}{2πr_{2}b_{2}}・・・(32)$$

(31),(32)式を(30)式に代入し整理すると、

$$\begin{align}H_{th}&=\frac{u_{2}}{g}(u_{2}-\frac{c_{r2}}{tanβ_{2}})\\&
=\frac{u_{2}^{2}}{g}(1-\frac{q}{2πr_{2}u_{2}b_{2}tanβ_{2}})・・・(33)\end{align}$$

(33)式となり、パラメータの変更ができました。

まとめ

高圧ガス甲種機械の検定試験範囲である、圧縮機・ポンプについてまとめました。

式の形だけ丸暗記するよりは、理論と導出方法から理解した方が良いと思います。

丸暗記する場合でも、式の単位を意識しておけば覚え間違いを防ぎやすくなります。