概要
熱と仕事に着目したエネルギー保存則を熱力学第一法則といいます。
熱を利用する場合、その形態は大きく2つに分けることができます。
- 物質の加熱など、熱そのものとして利用する。
- 熱を仕事に変換し、動力として利用する。
熱が仕事に変換できることは、産業革命の蒸気機関の発明時には経験的に知られていました。
熱力学の第一法則は、熱と仕事が互いに変換可能であり、熱も仕事もエネルギーの一形態だということを示した法則です。
一般式
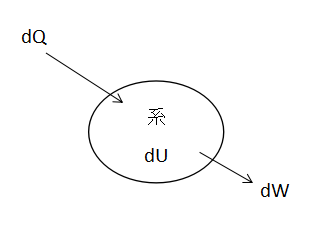
上図に示すように、ある系に熱量dQを加えることを考えます。
加えた熱量のうち、一部は温度上昇による内部エネルギーの増加dUに使用されます。
残りは外部への仕事dWとなります。したがって、
$$dQ=dU+dW・・・(1)$$
(1)式となります。
熱量dQを加える前を状態1、加えて平衡に達した後を状態2とすると、
$$\int_{1}^{2}dQ=\int_{1}^{2}dU+\int_{1}^{2}dW・・・(2)$$
(2)式となります。
ここで、内部エネルギーは状態量であるので、状態1から状態2への経路に依存せず、
$$\int_{1}^{2}dU=U_{2}-U_{1}=ΔU・・・(3)$$
(3)式のように表すことができます。
一方で、熱量や仕事は状態量ではないので、状態1から状態2への経路に依存するため、(3)式のように表すことはできません。
ここでは、熱量と仕事を、
$$\int_{1}^{2}dQ=Q_{12}・・・(4)$$
$$\int_{1}^{2}dW=W_{12}・・・(5)$$
Q12:状態1から状態2に変化するときの熱量
W12:状態1から状態2に変化するときの外部への仕事
(4)、(5)式のように表し、(3)、(4)、(5)式を(2)式に代入すると、
$$Q_{12}=ΔU+W_{12}・・・(6)$$
(6)式となります。(6)式が熱力学第一法則として一般的に知られている式です。
経路による熱量の違い
熱量や仕事は状態量ではなく、経路によって値が変化すると前述しました。
ここでは熱量を実際に計算し、経路によって本当に値が異なるのか確認してみましょう。
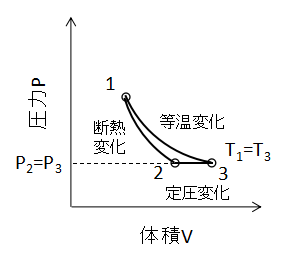
例として理想気体の状態変化について、状態1から状態3に変化するときの熱量を2種類の経路で算出します。
- 経路①:等温変化(状態1→状態3)
- 経路②:断熱変化(状態1→状態2)、定圧変化(状態2→状態3)
経路①、②のどちらも状態1から変化開始し、状態3で変化終了するところは同じです。
計算にあたって使用する物性値は窒素のものをベースとし、以下の条件が与えられているとします。
- 気体の質量m:1kg
- 気体定数R:8.314/28=0.297kJ/(kg・K)
- 定圧比熱容量Cp:1.04kJ/(kg・K)
- 比熱容量の比γ:1.4
- 状態1:圧力200kPa、温度300K、体積10m3
- 状態3:圧力100kPA、温度300K
経路①
経路①は等温変化で状態①から状態③へ変化します。
等温変化の場合、内部エネルギー変化ΔU=0となります。
したがって、(6)式は
$$Q_{経路①}=W_{経路①}=mRT_{3}{\rm{ln}}(\frac{V_{3}}{V_{1}})・・・(7)$$
(7)式となります。
ボイル・シャルルの法則から、等温変化なので、
$$P_{1}V_{1}=P_{3}V_{3}・・・(8)$$
$$V_{3}=20m^{3}$$
(8)式のように状態3の体積V3が計算できます。
求めたV3を(7)式に代入し、
$$Q_{経路①}=1×0.297×300×{\rm{ln}}(20/10)≒61.7kJ$$
経路①の熱量Qは61.7kJとなりました。
経路②
経路②はまず断熱変化で状態1から状態2に変化します。
断熱変化の場合、Q12=0となり、熱のやりとりはありません。
続いて、定圧変化で状態2から状態3に変化します。
定圧変化の場合、熱量Qは
$$Q_{23}=mc_{p}(T_{3}-T_{2})・・・(9)$$
(9)式で計算できます。
(9)式を使用するためには、状態2の温度T2を求める必要があります。
温度T2は状態1から状態2への断熱変化の式から算出します。
$$\frac{T_{2}}{T_{1}}=(\frac{P_{2}}{P_{1}})^{\frac{γ-1}{γ}}・・・(10)$$
(10)式を使用すると、T2=246Kとなりました。
あとはT2を(9)式に代入し、
$$Q_{23}=1×1.04×(300-246)≒56.1kJ・・・(11)$$
Q23=56.1kJとなりました。
したがって、経路②の熱量Qは、
$$Q_{経路②}=Q_{12}+Q_{23}=0+56.1=56.1kJ・・・(12)$$
(12)式から56.1kJとなります。
経路①と②を比較すると、
- 経路①の熱量Q=61.7kJ
- 経路②の熱量Q=56.1kJ
近い値にはなりましたが、完全には一致していませんね。
仮に熱量Qが状態量であれば、経路①と②の熱量が一致するはずです。
そのため、熱量Qは状態量ではない、ということが示せました。
おわりに
熱力学第一法則について解説しました。
熱や仕事を含めたエネルギー保存則で、特に熱機関を考えるうえでは重要な法則です。
