概要
粉じんやダスト、ミスト等の粒子を捕集する際によく使用されるのが、障害物に粉じん等を捕集させる方法です。
この方法の中でも特に、粒子をフィルターに衝突させて捕集する機構をフィルター集塵といいます。
他の捕集機構と比較して簡単であるため、エアフィルターやミストエリミネーターといった名称の装置として、プラントではよく使用されています。
このような捕集装置の設計はメーカーが普通実施しますが、ユーザー側もメーカーの設計仕様が妥当かどうか検討することもあるでしょう。
本記事ではフィルター集塵の効率について説明します。
フィルター効率
ここでは、繊維式のエアフィルターを例にしてフィルター効率(捕集効率)を考えてみます。
フィルター効率η
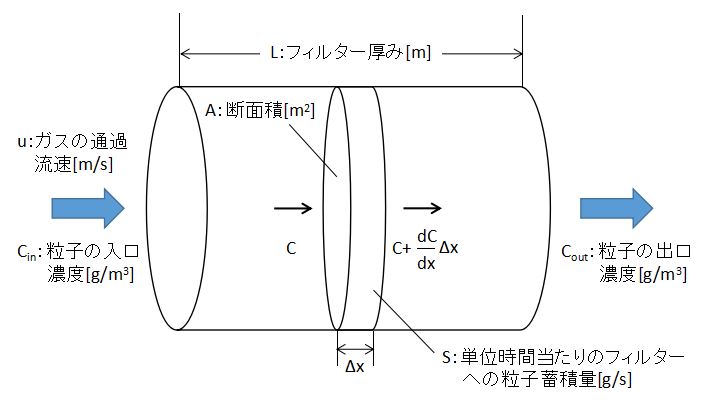
上図のように、ある粒子濃度Cの含じんガスが流速uで繊維式エアフィルターを通過し粒子が捕集されるとします。
このとき、フィルター内の微小区間で物質収支を取ると、
$$CuA-(C+\frac{dC}{dx}Δx)uA=S・・・(1)$$
C:粒子濃度[g/m3]、u:ガスの通過流速[m/s]、A:フィルター断面積[m2]
S:単位時間当たりのフィルターへの粒子蓄積量[g/s]
(1)式となります。
フィルターへの粒子蓄積量Sは、
$$\begin{align}S=(粒子の物質流束)&×(繊維円柱の流れに垂直な全断面積)\\&×(単一繊維捕集効率η_{t})・・・(2)\end{align}$$
(2)式で表されます。
粒子の物質流束[g/(m2・s)]は、フィルターの充填率α[-]とすると作用する流速はu/(1-α)となるので、
$$粒子の物質流束=C\frac{u}{1-α}・・・(3)$$
(3)式となります。
次に繊維円柱の流れに垂直な全断面積[m2]は、円柱の全長[m]×円柱の直径Df[m]となります。
円柱の全長は、円柱の占める体積α×AΔxを円柱の断面積で割れば得られるので、
$$繊維円柱の流れに垂直な全断面積=\frac{αAΔx}{\frac{π}{4}{D_{f}}^{2}}×D_{f}・・・(4)$$
(4)式となります。
(2)、(3)、(4)式から(1)式を整理すると、
$$\frac{dC}{dx}=-\frac{4α}{π(1-α)}\frac{1}{D_{f}}Cη_{t}・・・(5)$$
(5)式となります。
フィルターの入口濃度Cin、出口濃度Cout、フィルター厚さLとし、C=Cin~Cout、x=0~Lまで積分すると(6)式となります。
$${\rm{ln}}\frac{C_{out}}{C_{in}}=-\frac{4α}{π(1-α)}\frac{L}{D_{f}}η_{t}・・・(6)$$
フィルター効率ηは、
$$η=1-\frac{C_{out}}{C_{in}}・・・(7)$$
(7)式で表されます。
したがって、(6)式をフィルター効率ηで表すと(8)式となります。
$${\rm{ln}}(1-η)=-\frac{4α}{π(1-α)}\frac{L}{D_{f}}η_{t}・・・(8)$$
ちなみに(6)式のように粒子濃度がフィルター厚さに対して対数的に減少する傾向を対数透過則といいます。
この(8)式から、フィルター効率ηを向上させるためには、
- フィルター厚みLを厚くする。
- 繊維径Dfを小さくする。
などの方法が有効であることがわかります。
単一繊維捕集効率ηt
(8)式からフィルター効率ηが算出できますが、(8)式には単一繊維捕集効率ηtというパラメータが含まれています。
フィルター効率ηの算出には、このηtを求める必要があります。
ηtの算出は近似式を使用することが多く、様々な式が発表されています。
詳細は以下の記事で解説しています。
-

【単一繊維捕集効率】について解説:繊維1本当たりの粒子捕集効率
フィルターの繊維1本が粒子をどの程度捕集するかを表わす効率を単一繊維捕集効率といいます。フィルターの総合的な捕集効率を算出するためには、この単一繊維捕集効率が重要になってきます。単一繊維捕集効率は粒子の大きさやフィルター繊維径、充填率の値によって大きく変化します。
続きを見る
まとめ
フィルター集塵の効率について解説しました。
どのような操作をすれば粒子が捕集しやすくなるのかは直感的にはわかりますが、理論的にも理解しておいた方がよいでしょう。

