概要
カルノーサイクルは、2つの等温変化と2つの断熱変化を組み合わせたサイクルです。それぞれの変化は準静的過程であるため、カルノーサイクルは可逆的なサイクルとなっています。
また、カルノーサイクルは理論上最も熱効率が高いサイクルとされています。
そのため熱機関を考えるうえでは、まずカルノーサイクルを勉強しベースとすることが多いでしょう。
本記事ではカルノーサイクルの原理や熱効率について解説しています。
カルノーサイクルの原理
例としてシリンダー内のピストンの動きでカルノーサイクルの変化のイメージを示しました。
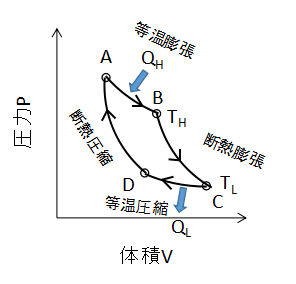
上のP-V線図の点Aからスタートし、1巡する場合を考えます。
①等温膨張過程(A⇒B)
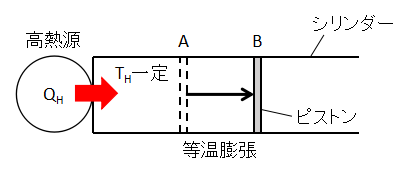
シリンダー内の流体を温度THの高熱源に接触させて、等温的に膨張させます。
このとき、流体は高熱源から熱量QHを吸収します。
②断熱膨張過程(B⇒C)
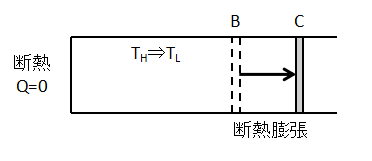
シリンダーから高熱源を離して、断熱的に膨張させます。
流体に熱の出入りがないため、膨張して仕事をするために気体の内部エネルギー(温度)が減少します。
③等温圧縮過程(C⇒D)

シリンダー内の流体を温度TLの低熱源に接触させて、等温的に圧縮します。
このとき、流体は低熱源に熱量QLを放出します。
④断熱圧縮過程(D⇒A)
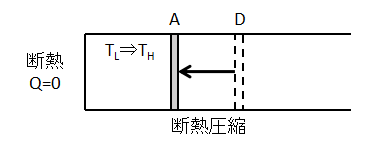
シリンダーから低熱源を離して、断熱的に圧縮します。
流体に熱の出入りがない状態で、外部から仕事をされるため、気体の内部エネルギー(温度)が増加します。
このような4種類の過程を経て、シリンダー内の気体は元の状態である点Aへと戻ります。
カルノーサイクルの熱効率
熱機関の効率は、供給された熱量に対して取り出された仕事の割合で定義されます。
この割合を熱効率、あるいはカルノー効率ηといい、(1)式で表されます。
$$η=\frac{W}{Q_{H}}・・・(1)$$
η:熱効率[-]、QH:高熱源から流体に供給された熱量[J]
W:外部へ取り出された仕事[J]
ここで、熱力学の第一法則について考えます。
$$Q=ΔU+W・・・(2)$$
サイクルが一巡して元の状態に戻った場合、状態量である内部エネルギーの変化ΔUはゼロとなります。
また、高熱源からQHを吸収し、低熱源にQLを放出しているので、シリンダー内の気体が受け取った正味の熱量Qは
$$Q=Q_{H}-Q_{L}・・・(3)$$
(3)式となります。
これらの関係から、(2)式における仕事Wは、
$$W=Q_{H}-Q_{L}・・・(4)$$
(4)式となります。(4)式を(1)式に代入すると、熱効率ηは、
$$η=\frac{Q_{H}-Q_{L}}{Q_{H}}=1-\frac{Q_{L}}{Q_{H}}・・・(5)$$
(5)式で表すことができます。
(5)式から、カルノーサイクルの熱効率ηは、高熱源から吸収する熱量QHと低熱源に放出する熱量QLのみで決定されることがわかります。
また、(5)式の導出過程においてはシリンダー内の流体に仮定を置いていませんから、理想的でない実在気体に対しても(5)式は成立します。
理想気体のカルノーサイクル
シリンダー内の流体が理想気体であると仮定した場合、カルノーサイクルで取り出せる仕事Wや熱効率ηを簡単に計算することができます。
1サイクルで外部にする仕事

上図にカルノーサイクルのP-V線図を示します。
等温過程、断熱過程のどちらも圧力P、体積Vが変化しますので、P-V線図では似通った曲線でサイクルが構成されます。
ここで、点A、B、C、Dにおける気体の体積をVA、VB、VC、VDとしたとき、カルノーサイクルで取り出せる仕事Wを体積Vで表してみましょう。
まずA⇒Bの等温膨張過程の仕事について考えます。
仕事の定義から、A⇒Bの仕事WABは
$$W_{AB}=\int_{V_{A}}^{V_{B}}PdV・・・(6)$$
(6)式となります。
次に、理想気体の状態方程式から、
$$PV=nRT・・・(7)$$
P:気体の圧力[Pa]、V:気体の体積[m3]、n:気体のモル量[-]
R:気体定数[J/(mol・K)]、気体の温度[K]
(7)式が成り立ちます。(7)式を(6)式に代入すると、
$$W_{AB}=\int_{V_{A}}^{V_{B}}\frac{nRT}{V}dV・・・(8)$$
(8)式となります。
ここで、等温過程なので温度Tは一定温度THとして扱えます。そのため、(8)式を体積Vについて積分することができます。
$$W_{AB}=nRT_{H}{\rm{ln}}\frac{V_{B}}{V_{A}}・・・(9)$$
よって、(9)式がA⇒Bの等温膨張過程で取り出せる仕事となります。
同様に、C⇒Dの等温圧縮過程についても式を立てます。
ほぼ同じ導出なので省略しますが、仕事WCDをWCD>0として求めると、
$$W_{CD}=nRT_{L}{\rm{ln}}\frac{V_{C}}{V_{D}}・・・(11)$$
(11)式となります。
次にB⇒Cの断熱膨張過程について式を立てます。
熱力学第一法則と断熱過程(δQ=0)であることから、
$$W_{BC}=-ΔU_{BC}・・・(12)$$
(12)式となります。
内部エネルギー変化ΔUBCは、定容比熱CVを用いて、
$$ΔU_{BC}=nC_{V}(T_{L}-T_{H})・・・(13)$$
(13)式で表せますから、仕事WBCは、
$$W_{BC}=-ΔU_{BC}=nC_{V}(T_{H}-T_{L})・・・(14)$$
(14)式となります。
同様に、D⇒Aの断熱圧縮過程についても式を立てます。
ほぼ同じ導出なので省略しますが、仕事WDAをWDA>0として求めると、
$$W_{DA}=nC_{V}(T_{H}-T_{L})・・・(15)$$
(15)式となります。
これで4つ全ての過程での仕事が求まりました。
最後に1サイクルで外部にする仕事Wは、WCDとWDAの値を正として求めたことに注意して、
$$\begin{align}W&=W_{AB}+W_{BC}-W_{CD}-W_{DA}\\&=nRT_{H}{\rm{ln}}\frac{V_{B}}{V_{A}}-nRT_{L}{\rm{ln}}\frac{V_{C}}{V_{D}}・・・(16)\end{align}$$
(16)式となります。
また、(16)式はポアソンの式を使用すればさらに簡略化できます。
まずB⇒Cの断熱膨張過程でポアソンの式を使用すると、
$$T_{H}{V_{B}}^{γ-1}=T_{L}{V_{C}}^{γ-1}・・・(17)$$
γ:比熱容量の比[-]
(17)式が成り立ちます。
同様にD⇒Aの断熱圧縮過程でポアソンの式を使用すると、
$$T_{H}{V_{A}}^{γ-1}=T_{L}{V_{D}}^{γ-1}・・・(18)$$
(18)式が成り立ちます。
(17)式÷(18)式とすることで、
$$\frac{V_{B}}{V_{A}}=\frac{V_{C}}{V_{D}}・・・(19)$$
(19)式となります。
(19)式で(16)式を簡略化すると、
$$W=nR(T_{H}-T_{L}){\rm{ln}}\frac{V_{B}}{V_{A}}・・・(20)$$
(20)式となり、1サイクルで取り出せる仕事Wを体積Vで表すことができました。
1サイクルで外部から吸収する熱量
1サイクルで外部から吸収する熱量も同様に計算できます。
断熱過程での熱の出入りはないので、実質は等温過程のみ考えればよいです。
熱力学の第一法則と、等温過程なのでΔU=0であることから、
$$Q=W・・・(21)$$
(21)式のように熱量Qと仕事Wは等しくなります。
したがって、1サイクルで外部から吸収する熱量Qは、
$$Q=W=nR(T_{H}-T_{L}){\rm{ln}}\frac{V_{B}}{V_{A}}・・・(21)$$
(21)式のように仕事Wと同じになります。
熱効率
理想気体における熱効率は、前述した実在気体の熱効率よりもわかりやすく表すことができます。
等温過程A⇒B、C⇒Dにおいては前述したようにQ=Wであるため、
$$Q_{H}=W_{AB}=nRT_{H}{\rm{ln}}\frac{V_{B}}{V_{A}}・・・(22)$$
$$Q_{L}=W_{CD}=nRT_{L}{\rm{ln}}\frac{V_{C}}{V_{D}}・・・(23)$$
(22)、(23)式が成立します。
(19)式を使用しつつ、(22)式÷(23)式を実施すると、
$$\frac{Q_{L}}{Q_{H}}=\frac{T_{L}}{T_{H}}・・・(24)$$
(24)式となります。
この(24)式を、前述した(5)式に代入すると、理想気体のカルノーサイクルの熱効率ηは、
$$η=1-\frac{Q_{L}}{Q_{H}}=1-\frac{T_{L}}{T_{H}}・・・(25)$$
(25)式で表されます。
(25)式から、理想気体のカルノーサイクルの熱効率は、高熱源温度THと低熱源温度TLのみで決定され、同一の熱源状態で得られる最高の熱効率となります。
また、明らかにTH>TLであるため、熱効率ηが100%となる熱機関は存在せず、熱量Qを仕事Wに100%変換できないことをカルノーサイクルは証明しています。
T-S線図
カルノーサイクルのT-S線図は非常に特徴的なので覚えやすいです。
A⇒Bの等温膨張過程においては、エントロピーの定義式ds=dq/Tから、
$$s_{AB}=\frac{Q_{H}}{T_{H}}・・・(26)$$
比エントロピーは(26)式となります。
同様にC⇒Dの等温圧縮過程では、
$$s_{CD}=-\frac{Q_{L}}{T_{L}}・・・(27)$$
(27)式となります。
(24)式から、熱量QH、QL、TH、TLの関係がわかっていますから、(26)、(27)式から、
$$s_{AB}=-s_{CD}・・・(28)$$
(28)式となります。
したがって、等温過程における比エントロピー変化sAB、sCDは値の絶対量は同じで符号が反対であることがわかります。
また、断熱過程ではdq=0となりますから、断熱過程における比エントロピー変化sBC、sDAは
$$s_{BC}=s_{DA}=0・・・(29)$$
(29)式となります。
したがって、温度T、エントロピーSからなるT-S線図は、
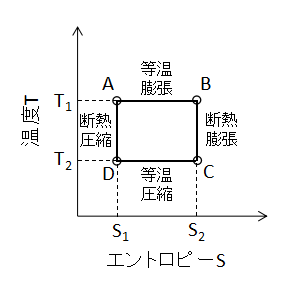
上図に示すような四角形のサイクルとなります。
等温過程では温度一定であるため、水平方向の変化となり、断熱過程では比エントロピー変化がゼロであるため、鉛直方向の変化となります。
おわりに
カルノーサイクルについて解説しました。
様々な資格試験に出題されるので、丸暗記ではなくちゃんと理論を理解した方が後々楽です。
