概要
粒子の慣性力と粘性抵抗の比を表わす無次元数をストークス数Stkといい、(1)式で表されます。
$$Stk=\frac{ρ_{p}u{d_{p}}^2}{18μL}・・・(1)$$
ρp:粒子密度[kg/m3]、u:代表流速[m/s]、dp:粒子径[m]
μ:流体粘度[Pa・s]、L:代表長さ[m]
Stk<<1だと、粒子は流体の流れに追随するとみなせます。
逆にStk>1だと、粒子は流体の流線から離れ、異なる運動をするようになります。
ストークス数は流体と粒子の運動の両方が重要になる単位操作において重要なパラメータとなることがあります。
粒子捕集におけるストークス数
集塵が最もストークス数を多用する分野かもしれません。
ストークス数の定義
まずはじめに、集塵の分野では代表長さの取り方でストークス数の値が異なるため注意が必要です。
$$粒子直径基準:Stk=\frac{C_{c}ρ_{p}u{d_{p}}^2}{18μd_{f}}・・・(2)$$
$$粒子半径基準:Stk=\frac{C_{c}ρ_{p}u{d_{p}}^2}{9μd_{f}}・・・(3)$$
Cc:カニンガムの補正係数[-]、df:フィルター繊維径[m]
(2)式もしくは(3)式のどちらかで表されることが多いです。その文献での定義をしっかり確認しましょう。
また、(3)式の粒子半径基準のストークス数を1/2で割った値を慣性パラメータψ[-]と定義し使用することがあります。
$$ψ=\frac{Stk}{2}=\frac{C_{c}ρ_{p}u{d_{p}}^2}{18μd_{f}}・・・(4)$$
慣性捕集機構
例えばフィルターによって気流中の粒子を除去する場合を考えます。
粒子が大きくなると(2)式からストークス数が大きくなるため、粒子に働く慣性力が大きくなることがわかります。
一般に粒子径が10μmより大きくなるとStk>1であることが多く、慣性捕集機構が支配的となります。
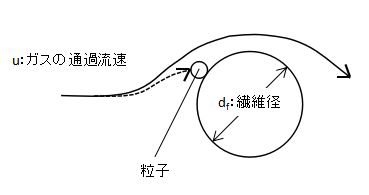
慣性捕集機構では、流体はフィルター繊維を避けて流れますが、粒子はフィルター繊維を避けきれずに衝突し捕集されます。
一方で、粒子径が0.1μmより小さくなるとSt<<1となることが多く、粒子に慣性力はほとんど働きません。
粒子は気流とほぼ同じ流線を辿るため、慣性捕集機構での粒子捕集は困難です。
この場合、ブラウン拡散を利用した拡散捕集機構の方がより支配的となり、フィルターも拡散捕集機構に適した仕様に変更する必要があります。
このように、集塵の分野ではストークス数により粒子の捕集機構を見極めます。
あるいは捕集効率の推算式にストークス数が含まれているものもあり、非常に重要な無次元数となっています。
撹拌槽におけるストークス数
撹拌の分野でもストークス数を確認することがあります。最も多いのは固液撹拌でしょう。
撹拌翼による吐出流の流れに、粒子がどのくらい追随して流動するのかは気になるところです。
粒子径が十分に小さければSt<<1となり、粒子は吐出流れに追随するため均一分散が比較的達成しやすいです。
一方で、粒子径や粒子の密度が大きいとSt>1となり、粒子は吐出流れに追随しません。
固液撹拌は液体より比重の重い粒子を扱うことが多いので、St>1の場合は底に沈んだまま滞留する状態となります。
例えば流通式撹拌槽においてオーバーフローで液体を抜き出す場合は注意しなければなりません。
一方で底に粒子が沈んだままでも、撹拌翼の回転数を浮遊限界撹拌速度Njs以上に保っておけばある程度の物質移動は行われるので、強いて均一分散にする必要性はない、という考え方もあります。
まとめ
ストークス数Stkについて解説しました。
流体と粒子どちらも扱う場合には、ストークス数で整理すると1つの指標となるかもしれません。
