概要
ある化学変化によって起こるエンタルピー変化量は、その反応が1段階で起ころうとも多段階で起ころうとも、同じ値を示します。
途中で様々な中間反応が起こったとしても、最終的に同じ化学変化の状態に行き着くならばエンタルピー変化量は同じとなります。
これをHess(ヘス)の法則といいます。この法則を利用することで既知の反応熱から未知の反応熱を算出することができます。
この記事ではHessの法則の計算法について解説します。
反応熱の計算方法
炭素Cの燃焼反応
例として、炭素Cが燃焼して二酸化炭素CO2になる反応について考えます。
炭素Cが完全燃焼すると、
$$C(s)+O_{2}(g)→CO_{2}(g)・・・(1)$$
(s):固体、(g):気体
(1)式となりCO2が生成します。。
一方で不完全燃焼だと、
$$C(s)+\frac{1}{2}O_{2}(g)→CO(g)・・・(2)$$
(2)式のように一酸化炭素COが発生します。
COはさらに燃焼して
$$CO(g)+\frac{1}{2}O_{2}(g)→CO_{2}(g)・・・(3)$$
(3)式でCO2となります。
仮に(1)式の反応熱ΔH1=-394kJ/mol、(2)式の反応熱ΔH2=-111kJ/molがわかっている場合、Hessの法則から(3)式の反応熱を計算できます。
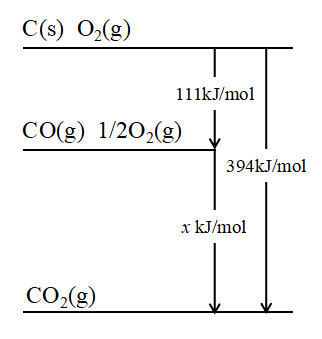
上図にHessの法則を考える際のイメージ図を示します。
(1)式で炭素Cから一気にCO2が生成する場合は394kJ/mol発熱します。
一方で炭素Cから不完全燃焼でCOが生成する場合は(2)式から111kJ/mol発熱します。さらに(3)式でCOが燃焼しCO2が生成しますが、最終的には同じ生成物CO2(g)に行き着きます。
このとき、Hessの法則からエンタルピー変化量は同じになりますから、(2)式の反応熱をxkJ/molとすると、
$$-111+x=-394$$
$$x=-283kJ/mol$$
となります。
プロピレンの燃焼反応
炭素Cの燃焼反応は化学式が簡単な形だったので反応熱の差し引きだけでわかりやすく求められます。
しかし3つ以上の化学式にHessの法則を当てはめる場合は、中間生成物と最終反応物との関係がわかりにくいので化学式を足し引きした方がよいでしょう。
例として、プロピレンの燃焼反応熱を求めてみましょう。
$$C_{3}H_{6}(g)+\frac{9}{2}O_{2}(g)→3CO_{2}(g)+3H_{2}O(l)・・・(4)$$
$$C_{3}H_{8}(g)+5O_{2}(g)→3CO_{2}(g)+4H_{2}O(l)・・・(5)$$
$$C_{3}H_{6}(g)+H_{2}(g)→C_{3}H_{8}(g)・・・(6)$$
$$H_{2}(g)+\frac{1}{2}O_{2}(g)→H_{2}O(l)・・・(7)$$
(s):固体、(l):液体、(g):気体
プロピレンC3H6の燃焼反応は(4)式で表されます。
ここでは(5)~(7)式の反応熱がそれぞれΔH5=-2220kJ/mol、ΔH6=-124kJ/mol、ΔH7=-286kJ/molとわかっているものとします。
化学式を足し引きする場合は、化学式を等号に変換して反応熱を式中に加えて考えるとわかりやすいです。
(5)~(7)式を、
$$C_{3}H_{8}(g)+5O_{2}(g)=3CO_{2}(g)+4H_{2}O(l)-2220kJ/mol・・・(8)$$
$$C_{3}H_{6}(g)+H_{2}(g)=C_{3}H_{8}(g)-124kJ/mol・・・(9)$$
$$H_{2}(g)+\frac{1}{2}O_{2}(g)=H_{2}O(l)-286kJ/mol・・・(10)$$
(8)~(10)式として考えます。
後は普通の方程式と同様の式変形で(4)式の形を導きます。
(8)+(9)-(10)式とすると、
$$\begin{align}&C_{3}H_{8}(g)+5O_{2}(g)+C_{3}H_{6}(g)+H_{2}(g)-(H_{2}(g)+\frac{1}{2}O_{2}(g))\\&=3CO_{2}(g)+4H_{2}O(l)+C_{3}H_{8}(g)-(H_{2}O(l))-2220-124-(-286)\end{align}$$
$$C_{3}H_{6}(g)+\frac{9}{2}O_{2}(g)=3CO_{2}(g)+3H_{2}O(l)-2058kJ/mol$$
このように(4)式の形が導き出せました。
反応熱の部分も式変形の過程で同様に計算すると、-2058kJ/molとなりこれが(4)式の反応熱となります。
おわりに
Hessの法則を使用した計算方法について解説しました。
実務では文献には載っていない未知の反応の反応熱を見積もる場合に使用することが多いでしょう。
