概要
本記事ではPythonの線形最小二乗法の計算例としてアレニウスプロットををやってみました。
単純にアレニウスプロットをやるだけならExcel等の表計算ソフトを使用する方が便利です。
Pythonで最小二乗法をやる場合は計算手法まできちんと記述しないといけませんから、Excelよりも難易度が上がります。
その分、最小二乗法に対する理解も深まりますから勉強としては良いと思います。
原理
原理についてはこちらの記事で途中まで解説しています。

$$S=\sum_{n=1}^{n}(y_{i}-(ax_{i}+b))^{2}・・・(1)$$
(1)式の誤差の二乗和Sが最小になるよう定数a,bを決定します。
具体的には(1)式をa,bに関して偏微分した値がゼロになれば最小値となります。
それぞれ偏微分すると、
$$\frac{∂S}{∂a}=\sum_{n=1}^{n}(2x_{i}^{2}a-2x(y-b))=0・・・(2)$$
$$\frac{∂S}{∂b}=\sum_{n=1}^{n}(2b-2(y_{i}-ax_{i}))=0・・・(3)$$
(2)、(3)式が成り立ちます。
(3)式から、
$$b=\frac{1}{n}\sum_{n=1}^{n}(y_{i}-ax_{i})・・・(4)$$
bを(4)式で表せます。(4)式を(2)式に代入してbを消去して整理すると、
$$a=\frac{\displaystyle\sum_{n=1}^{n}x_{i}y_{i}-\frac{1}{n} \sum_{n=1}^{n} x_{i}\sum_{n=1}^{n} y_{i}}{\displaystyle\sum_{n=1}^{n} x_{i}^{2}-\frac{1}{n}(\sum_{n=1}^{n}x_{i})^{2}}・・・(5)$$
(5)式となります。
したがって、y=ax+bの形の直線近似に関しては(4)、(5)式を使用すればa、bを解析的に決定できることになります。
Pythonでの計算法
計算条件
こちらの記事で計算しているアレニウスプロットをPythonでも計算してみます。
| T[K] | k[m3/(mol・s)] |
| 698.2 | 5.088E-4 |
| 740.2 | 1.506E-3 |
| 818.2 | 7.770E-3 |
| 887.2 | 2.678E-2 |
上表に示すデータから活性化エネルギーEと頻度因子Aを決定します。
アレニウスプロットは
$${\rm{ln}}k={\rm{ln}}A-\frac{E}{R}\frac{1}{T}・・・(6)$$
(6)式で表されます。y=ax+bと比較すると、
$$a=-\frac{E}{R}・・・(7)$$
$$b={\rm{ln}}A・・・(8)$$
定数a、bはそれぞれ(7)、(8)式となります。
ライブラリ・モジュールのインポート
NumpyとMatplotlibをインポートします。
#モジュールインポート
import numpy as np
import matplotlib.pyplot as plt前提条件
温度T、反応速度定数k、気体定数R、1/T、lnkをそれぞれ入力します。
#前提条件
T=np.array([698.2, 740.2, 818.2, 887.2])
k=np.array([5.088e-4,1.506e-3,7.77e-3,2.678e-2])
R=8.314
invT=1/T
lnk=np.log(k) 線形最小二乗法の入力
メインの線形最小二乗法を入力します。
#線形最小二乗法
def lls(invT,lnk):
n=len(invT) #データ数の取得
a=((np.dot(invT,lnk)-lnk.sum()*invT.sum()/n)/((invT**2).sum()-invT.sum()**2/n))
b=(lnk.sum()-a*invT.sum())/n
return a,b3行目でデータの点数を取得しています。
4行目で(5)式のaに関する式、5行目で(4)式のbに関する式を入力しています。
活性化エネルギー・頻度因子の計算
自分で定義したlls関数を使用して活性化エネルギーと頻度因子を計算します。
活性化エネルギー、頻度因子の計算
a,b=lls(invT,lnk)
E=-a*R #[J/mol]
A=np.exp(b) #[m3/(mol・s)]
print('E:{0:7.0f},,A:{1:6.0f}'.format(E,A))2行目でlls関数を使用しa、bの値を求めます。
3行目でaの値から活性化エネルギーEを求めます。
4行目でbの値から頻度因子Aを求めます。
5行目で求めたE、Aの値をprint関数で出力します。
グラフ用の入力
アレニウスプロットがきちんとできているかを確認します。
グラフ用
x_lin=np.linspace(0.001,0.002,num=20)
y_lin=a*x_lin+b
plt.plot(invT,lnk,'o')
plt.plot(x_lin,y_lin,'-')
plt.xlabel('1/T')
plt.ylabel('lnk')
plt.legend(['row data','linear plot'])
plt.show()2行目でプロットしたい横軸の範囲でxの値を生成します。ここでは0.001~0.002までの間を20分割して値を取得しています。
3行目でアレニウスプロットのyの値を計算しています。
5行目以降で元データと先ほど生成したxとyの値をプロットし、軸ラベルと凡例を設定しています。
計算結果の確認
特に入力ミス等がなければ以下のように結果が表示されます。
E: 107670,A: 58535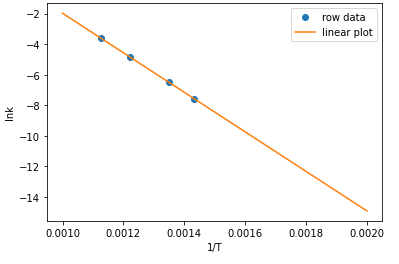
活性化エネルギーEと頻度因子Aの値はこちらの記事で求めたときの値とほぼ同じになりましたね。
グラフもきちんと線形プロットできています。
全体のコードを下に載せておきます。
#モジュールインポート
import numpy as np
import matplotlib.pyplot as plt
#前提条件
T=np.array([698.2, 740.2, 818.2, 887.2])
k=np.array([5.088e-4,1.506e-3,7.77e-3,2.678e-2])
R=8.314
invT=1/T
lnk=np.log(k)
#線形最小二乗法
def lls(invT,lnk):
n=len(invT) #データ数の取得
a=((np.dot(invT,lnk)-lnk.sum()*invT.sum()/n)/((invT**2).sum()-invT.sum()**2/n))
b=(lnk.sum()-a*invT.sum())/n
return a,b
#活性化エネルギー、頻度因子の計算
a,b=lls(invT,lnk)
E=-a*R #[J/mol]
A=np.exp(b) #[m3/(mol・s)]
print('E:{0:7.0f},,A:{1:6.0f}'.format(E,A))
#グラフ用
x_lin=np.linspace(0.001,0.002,num=20)
y_lin=a*x_lin+b
plt.plot(invT,lnk,'o')
plt.plot(x_lin,y_lin,'-')
plt.xlabel('1/T')
plt.ylabel('lnk')
plt.legend(['row data','linear plot'])
plt.show()まとめ
アレニウスプロットを例にPythonで線形最小二乗法について計算しました。
簡単ではありますが実務でもよく使う手法なので覚えておきましょう。
