概要
この記事では高圧ガス甲種機械の出題分野である、流体の流れについて解説します。
流体の流れは毎年春(5月頃)に実施される検定試験、秋(11月頃)の国家試験の両方に出題されており、重要な分野です。
ただし、問題の形式が検定試験と国家試験で大きく異なります。
同じ分野でも国家試験の方が明らかに難しく、検定試験の方が簡単です。
ここでは検定試験の流体の流れについて解説します。
流体の流れの出題分野
流体の流れは学識の大問5問中の1問です。
他の大問と比較して、流体の流れは簡単なので確実に点を取りたいところです。
問題構成としては、小問が10問前後あり、語句の記述もしくは計算値を入力します。
語句の記述は選択肢がないため、単に覚えているかどうかで決まります。
計算問題は検定試験の場合、簡単な問題が多いので楽です。
出題内容については、
・レイノルズ数
・層流と乱流
・連続の式
・ベルヌーイの定理
以上の4つは出題頻度が高く確実に覚えておきたいところです。
それ以外の内容は年ごとに出題内容が変わっているため予測が難しいです。
どこまで詳細な内容を詰めるかは、他の分野の勉強時間も考えて決めましょう。
以下に検定試験で過去に出題された内容をまとめました。
レイノルズ数
定義
$$Re=\frac{ρdu}{μ}=\frac{du}{ν}・・・(1)$$
Re:レイノルズ数[-]、ρ:流体密度[kg/m3]、d:配管直径[m]
u:流体の流速[m/s]、μ:流体粘度[Pa・s]、ν:動粘度[m2/s]
頻出です。レイノルズ数に関する様々な問題が出題されています。
過去の出題パターンとしては、
・(1)式の右辺を記述する。
・(1)式を使用してレイノルズ数を計算する。
・層流、乱流の閾値を回答する。
などがありました。
層流・乱流の閾値
層流、乱流の閾値は、
・層流:Re<2100
・遷移域:2100<Re<4000
・乱流:Re>4000
となっています。
相当直径
レイノルズ数の計算で使用する配管直径dについて、管の断面が円形でない場合は相当直径Deを使用します。
$$D_{e}=\frac{4A}{L_{p}}・・・(2)$$
De:相当直径[m]、A:流路の断面積[m2]、Lp:ぬれ辺長[m]
層流・乱流の最大流速
層流・乱流の最大流速と平均流速には次のような関係があります。
$$層流:\bar{u}=\frac{1}{2}u_{max}・・・(3)$$
$$乱流:\bar{u}=0.817u_{max}・・・(4)$$
層流の場合は理論的に(3)式を導出することができますが、乱流の(4)式は実験値です。
層流の1/2や乱流の0.817を答える問題がたまに出題されています。
連続の式
流体が定常的に流れている場合は、流路のどの位置でも流量が一定になる関係を連続の式といいます。
$$q_{m}=ρ_{1}A_{1}\bar{u_{1}}=ρ_{2}A_{2}\bar{u_{2}}・・・(5)$$
qm:質量流量[kg/s]
密度ρをかけて質量流量[kg/s]に変換していますが、問題文で体積流量[m3/s]が与えられた場合は密度をかける必要がありません。
問題文で与えられる単位系に応じて使用しましょう。
ベルヌーイの定理
流体のエネルギー保存則を非圧縮性流体に適用したものをベルヌーイの定理といいます。
単位によって(6)~(8)式に使い分けれらます。
・圧力[Pa]
$$\frac{1}{2}ρ_{1}\bar{u_{1}}^{2}+ρ_{1}gh_{1}+p_{1}=\frac{1}{2}ρ_{2}\bar{u_{2}}^{2}+ρ_{2}gh_{2}+p_{2}・・・(6)$$
・ヘッド[m]
$$\frac{\bar{u_{1}}^{2}}{2g}+h_{1}+\frac{p_{1}}{ρg}=\frac{\bar{u_{2}}^{2}}{2g}+h_{2}+\frac{p_{2}}{ρg}・・・(7)$$
・単位質量当たりのエネルギー[J/kg]
$$\frac{\bar{u_{1}}^{2}}{2}+gh_{1}+\frac{p_{1}}{ρ}=\frac{\bar{u_{2}}^{2}}{2}+gh_{2}+\frac{p_{2}}{ρ}・・・(8)$$
h1,h2:基準からの高さ[m]、g:重力加速度[m/s2]、p1,p2:圧力[Pa]
計算問題で出やすいのは、連続の式かこのベルヌーイの定理です。
ベルヌーイの定理について詳しくは下の記事で解説しています。

ファニングの式
乱流において、直管の圧力損失はファニングの式(9)式で計算できます。
$$ΔP=4f\frac{ρu^{2}}{2}\frac{L}{d}・・・(9)$$
ΔP:圧力損失[Pa]、f:摩擦係数[-]、ρ:流体密度[kg/m3]
u:流体の平均速度[m/s]、L:配管長さ[m]、d:配管直径[m]
出題頻度はそれほど高くないようですが、実務で使うことが多いので覚えておいて損はないです。
ファニングの式は下の記事で詳細に解説しています。

ハーゲン・ポアズイユの式
層流において、直管の圧力損失はハーゲン・ポアズイユの式(10)式で計算できます。
$$ΔP=\frac{32μLu}{d^{2}}・・・(10)$$
ΔP:圧力損失[Pa]、μ:流体粘度[Pa・s]
u:流体の平均速度[m/s]、L:配管長さ[m]、d:配管直径[m]
(10)式は理論的に導出することができるものの、少し時間がかかるので覚えておくことを推奨します。
ただ、出題頻度はあまり高くありません。
ちなみに、ハーゲン・ポアズイユの式は下の記事で詳細に解説しています。

トリチェリの定理
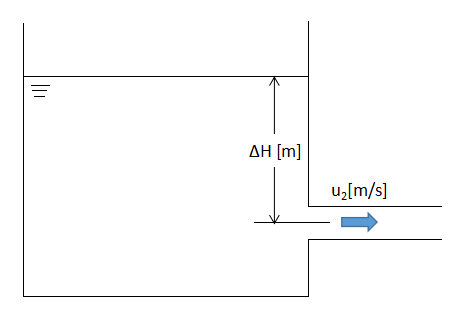
上図のような十分な大きさのタンク側面から液が流出する場合にトリチェリの定理(11)式が成り立ちます。
$$u_{2}=\sqrt{2gΔH}・・・(11)$$
u2:側面からの流出速度[m/s]、g:重力加速度[m/s2]
ΔH:流出位置から液面までの高さ[m]
(11)式はベルヌーイの定理から簡単に導出することができますが、式自体は簡単なので覚えておいでもよいでしょう。
まとめ
高圧ガス甲種機械の検定試験範囲である、流体の流れについてまとめました。
最低限、出題頻度の高い4項目(レイノルズ数、層流と乱流、連続の式、ベルヌーイの定理)についてはマスターしておきましょう。
