概要
最初に原料を全て反応器に仕込み反応させるタイプの反応器を回分式反応器をいいます。
最も手軽でわかりやすい反応器と言ってよいでしょう。
ラボスケールで何かを反応させる場合は、たいてい回分式反応器となります。
最初から生産性を考えて実験条件を設定するのは難しいですからね。
ただ、実機でも少量多品種な製品を製造するときは回分式反応器が向いています。
特にこのご時世は、機能性材料をユーザーに合わせてグレードを変えて製造する傾向にありますから、むしろ回分式反応器を設計する機会は増えるかもしれません。
連続式反応器より運転は複雑なので、設計難易度は回分式反応器の方が高いと思っています。
回分式反応器の基礎式
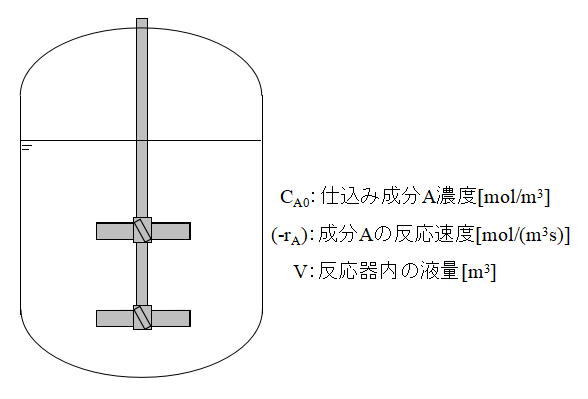
上図のような回分式反応器を考え、原料成分Aについて式を立てます。
流入・流出量はどちらもゼロです。
したがって、成分Aが反応で消費される速度がそのまま成分A濃度の時間変化と一致します。
$$(-r_{A})V=-V\frac{dC_{A}}{dt}・・・(1)$$
成分Aは消費され減少していくため、右辺はマイナスを付けるのがポイントです。
(1)式をt=0~tまで積分すると、
$$\int_{0}^{t}dt=-\int_{C_{A0}}^{C_{A}}\frac{dC_{A}}{(-r_{A})}$$
$$t=\int_{C_{A}}^{C_{A0}}\frac{dC_{A}}{(-r_{A})}・・・(2)$$
(2)式となります。
反応速度が判明している場合には、(2)式に代入することで成分Aが所定の濃度になるまでの時間を算出することができます。
1次反応や2次反応の場合には(2)式で積分することができ、解析的に答えを求められます。
また、成分Aの濃度と反応率は
$$C_{A}=C_{A0}(1-x_{A})・・・(3)$$
(3)式の関係にあり、(2)式をxAの積分式で表すこともできます。
(3)式を微分すると、
$$dC_{A}=-C_{A0}x_{A}・・・(4)$$
(4)式となります。
t=0のときCA=CA0でxA=0、t=tのとき、CA=CA、xA=xAとなりますので積分区間を変換し、(4)式を(2)式に代入します。
$$t=-\int_{x_{A}}^{0}\frac{dx_{A}}{(-r_{A})}$$
$$t=\int_{0}^{x_{A}}\frac{dx_{A}}{(-r_{A})}・・・(5)$$
(5)式となり、所定の反応率を達成するために必要な時間を算出することができます。
実務における回分式反応器のポイント
洗浄のしやすさ
回分式反応器は1バッチごとにグレードを切り替えることもあり、反応器内を洗浄することがよくあります。
そのため、反応器内部が洗浄しやすい構造かどうかというのは非常に重要です。
洗浄は水による高圧ジェットで行なうことが多いと思います。
しかしジェットがうまく当たらないような領域があると、そこに汚れが蓄積したり、次のバッチに混ざってしまうことが懸念されます。
したがって反応器内の内部品である、撹拌翼、バッフル、コイル、計器類はなるべく構造が簡単なものの方が回分式には向いています。
グレード変更による物性変化
複数グレード・多品種で生産する場合は、液の物性が大きく変化する可能性があります。
特に重要な物性は粘度で、反応器内の混合状態に大きく影響します。
粘度が高くなってしまうと反応器内の濃度分布、温度分布がより顕著になり、不均一な反応場となってしまいます。
反応率の低下、副反応の増加で収まるならまだ良い方で、温度制御が困難になると運転できなくなります。
反応器の設計段階で予めグレードの変更が予想される場合には、広い粘度範囲に対応できる撹拌翼を選定しておくことで対応できます。
