【移動単位数(NTU)】の計算方法を解説：吸収塔の塔高計算に使用

概要

移動単位数(NTU)とは吸収塔内での吸収操作の難しさを表わす無次元量です。

吸収効率が大きい(要求されるスペックが厳しい)、または吸収の推進力が小さいほどNTUは大きくなります。つまり、吸収が難しいほど値が大きくなります。

NTUは吸収塔の塔高計算をする際に必要なパラメータであり、本記事ではNTUの計算方法について紹介します。

NTUは通常、積分することによって求めますが、条件によっては計算が簡単になることがありますので、代表的な例について場合分けして紹介します。

NTUの計算方法

充填塔の塔高計算の記事で紹介していますが、NTUは4つの式で算出できます。

ここでは例としてN_OGについて考えます。

操作線、平衡線が曲線の場合

N_OGは(1)式で表されます。

$$N_{OG}=\int_{y_{AT}}^{y_{AB}}\frac{dy_{A}}{(y_{A}-y_{A}^{*})}・・・(1)$$

まず、積分項のy_A-y_A*について考えてみます。

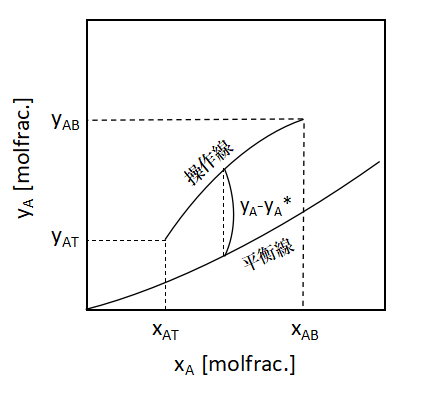
y_A-y_A*は上の図において、x_AT～x_ABの範囲内での任意のx_Aにおける操作線と平衡線のy_Aの差が
y_A-y_A*となります。

したがって、(1)式の1/(y_A-y_A*)の積分は、操作線の式と平衡線の式がわかれば計算できます。

操作線の式

操作線の式は一般に、

$$G(\frac{y_{A}}{1-y_{A}}-\frac{y_{AT}}{1-y_{AT}})=L(\frac{x_{A}}{1-x_{A}}-\frac{x_{AT}}{1-x_{AT}})・・・(2)$$

(2)式で表されます。
上図のように縦軸y_A、横軸x_Aとしてプロットすると曲線となります。

平衡線の式

平衡線の式は一般にHenryの法則から、

$$y_{A}^{*}=mx_{A}・・・(3)$$

(3)式で表されます。
(3)式だと一見すると、直線に見えます。

しかし、ガス吸収によって激しく発熱するような系では、塔頂から塔底の間で温度分布が付くため、Henry定数mが温度依存により変化します。
この効果により(3)式は傾きmが変化するため曲線となります。

(2)、(3)式から1/(y_A-y_A*)を算出し、解析的に積分できる場合は積分してN_OGを求めます。

積分できない場合は、微小区間に細かく分割して1/(y_A-y_A*)を算出し、全ての区間を足し合わせる(図積分する)ことでN_OGを求めることができます。

しかし実際は操作線、平衡線が両方曲線のケースは限られると思います。
吸収塔の用途として多いのが排ガス処理ですが、吸収させる排ガス濃度はそれほど高くないことが多く、たいていは直線近似できます。

操作線、平衡線が直線とみなせる場合

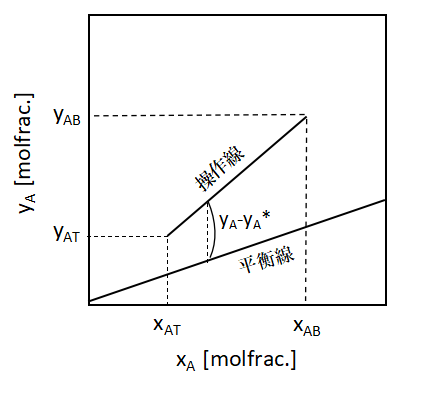
操作線の式

ガス吸収量が比較的小さい場合は、(2)式において

$$\frac{y_{A}}{1-y_{A}}≒y_{A}$$

$$\frac{y_{AT}}{1-y_{AT}}≒y_{AT}$$

$$\frac{x_{A}}{1-x_{A}}≒x_{A}$$

$$\frac{x_{AT}}{1-x_{AT}}≒x_{AT}$$

上の4式のように近似して簡略化できます。
結果、(2)式は(4)式のような形となり直線となります。

$$G(y_{A}-y_{AT})=L(x_{A}-x_{AT})$$

$$y_{A}=\frac{L}{G}(x_{A}-x_{AT})+y_{AT}・・・(4)$$

平衡線の式

ガスの吸収量が少ない場合は、塔内の温度は一定としてもよいです。
その場合には、(3)式のHenry定数mは一定値となり、直線となります。

$$y_{A}^{*}=mx_{A}・・・(3)$$

このように操作線、平衡線が直線とみなせる場合は、(1)の積分式を簡略化することができます。
ここでは導出は省きますが、

$$N_{OG}=\frac{y_{AB}-y_{AT}}{Δy_{lm}}=\frac{y_{AB}-y_{AT}}{\frac{(y_{AB}-y_{AB}^{*})-(y_{AT}-y_{AT}^{*})}{{\rm{ln}}\frac{y_{AB}-y_{AB}^{*}}{y_{AT}-y_{AT}^{*}}}}・・・(5)$$

(5)式となり、N_OGを求めることができます。

液流量が大きく分圧がある場合

液流量を増やしていくと、(4)式の直線の傾きであるL/Gが増大します。

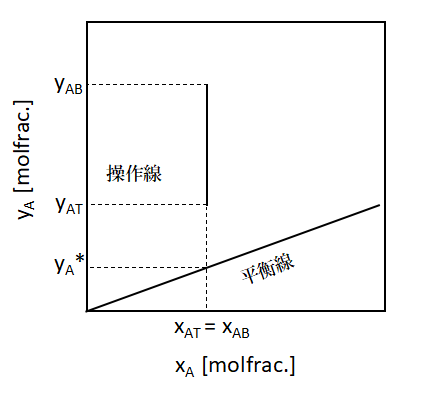
液流量が十分に大きい場合は、上図に示すように操作線は垂直な線になります。
このとき、y_A*はyの値によらず一定値を示しますから、y_A*はyの関数ではなくなることがわかります。

したがって(1)式を簡単に積分できるようになります。

$$N_{OG}=\int_{y_{AT}}^{y_{AB}}\frac{dy_{A}}{(y_{A}-y_{A}^{*})}=[{\rm{ln}}(y_{A}-y_{A}^{*})]^{y_{AB}}_{y_{AT}}\\ ={\rm{ln}}\frac{y_{AB}-y_{A}^{*}}{y_{AT}-y_{A}^{*}}・・・(6)$$

積分すると(6)式となり、N_OGを簡単に求めることができます。

ちなみに、液流量を増大させる場合は、吸収水をワンパスで流してしまうのは効率が良くないので、塔底液を塔頂へ循環させて液量を増やすのが効率が良いです。

液流量が大きく分圧がゼロの場合

溶解度が高く、瞬時にガスが液に溶ける場合は平衡分圧がゼロに近くなります。
この場合はy_A*≒0となりますから、(6)式に代入すれば、

$$N_{OG}={\rm{ln}}\frac{y_{AB}}{y_{AT}}・・・(7)$$

(7)式となり、より簡単にN_OGを算出することができます。

計算例

操作線、平衡線が直線とみなせる場合について、図積分による方法と(5)式を使用する方法でN_OGを算出してみます。

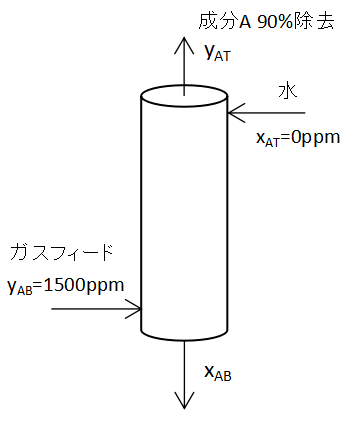
上図のような吸収塔で、濃度1500ppmの成分Aを25℃の水で90%吸収除去するときのN_OGを計算します。
ただし、L/G=40.3、Henry定数m=33とします。

成分A濃度1500ppmを90%除去しますから、塔頂の出口A濃度y_ATは残り10%の150ppmになります。

また、A濃度は微小なので操作線は(4)式を使用します。

$$y_{A}=\frac{L}{G}(x_{A}-x_{AT})+y_{AT}・・・(4)$$

(4)式を使用して、塔底での液中A濃度x_ABを算出します。

$$1500=40.3(x_{AB}-0)+150$$

$$x_{AB}≒33.5ppm$$

また、(3)式のHenry定数の式から、

$$y_{A}^{*}=33x_{A}・・・(3)$$

(3)、(4)式から1/(y_A-y_A*)は、

$$y_{A}-y_{A}^{*}=40.3(x_{A}-0)+150-33x_{A}=7.3x_{A}+150$$

$$\frac{1}{y_{A}-y_{A}^{*}}=\frac{1}{7.3x_{A}+150}・・・(8)$$

(8)式となります。
ここで、1/(y_A-y_A*)をy_Aについてy_AT～y_ABの間で図積分します。

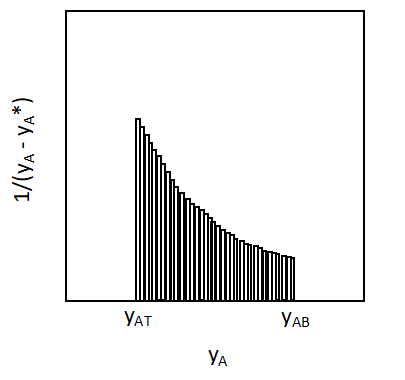
図で表すと上のようになります。

ただし、(8)式はx_Aについての関数になっているので、dy_Aをdx_Aの式に置き換える必要があります。
(4)式を微分することでdyとdxの関係式を求めると(10)式となります。

$$dy_{A}=40.3dx_{A}・・・(10)$$

1区間当たりの長方形の横の長さはdy_A、縦の長さは1/(y_A-y_A*)となります。

仮にx_Aの刻みを1として、縦軸1/(y_A-y_A*)はエクセル等で各区間の値を算出し、全ての区間を足し合わせると、

$$N_{OG}≒0.136×40.3×1≒5.47$$

となり、N_OGを算出できました。
積分の刻みをもっと細かくすれば精度が良くなります。

続いて、(5)式を使用してN_OGを算出します。

算出にあたっては平衡値y_AB*、y_AT*を(3)式で算出します。

$$y_{AB}^{*}=33×33.5≒1106ppm$$

$$y_{AT}^{*}=33×0=0ppm$$

したがって、(5)式から、

$$N_{OG}=\frac{y_{AB}-y_{AT}}{\frac{(y_{AB}-y_{AB}^{*})-(y_{AT}-y_{AT}^{*})}{{\rm{ln}}\frac{y_{AB}-y_{AB}^{*}}{y_{AT}-y_{AT}^{*}}}} =\frac{1500-150}{\frac{(1500-1106)-(150-0)}{{\rm{ln}}(\frac{1500-1106}{150-0})}}≒5.34$$

図積分で求めた値と近くなりましたね。
一般には(5)式を使用して求める方が簡単なので、簡略式を使用できる場合はそちらを使いましょう。