概要
超音波式流量計は超音波が流体の流速により伝播時間や周波数が変化することを利用して流量を測定します。
配管の外側から取り付けて超音波を照射し配管内の流体流速を測定できるタイプ(クランプオン型)があるため、元から流量計が設置されていない配管の流量測定で重宝します。
この記事では超音波式流量計の特徴を解説しています。
原理
伝播速度差方式
超音波の伝播速度から流速及び流量を計算する方式です。
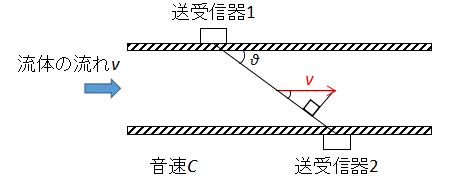
超音波送受信機は上図のように配管に対して斜めに取り付けます。
中の流体が流れていないと超音波は音速Cで伝播します。一方で、流体に流れがあると送信の方向によって超音波の伝播速度及び伝播時間が変化します。
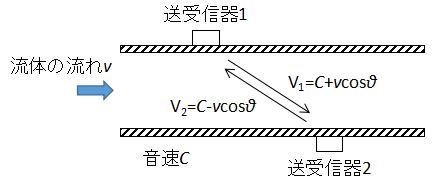
送受信器1⇒送受信器2の場合、
$$V_{1}=C+v\rm{cos}θ・・・(1)$$
送受信器2⇒送受信器1の場合、
$$V_{2}=C-v\rm{cos}θ・・・(2)$$
となります。
送受信器間の距離をLとすると、伝播時間t1、t2は(3)、(4)式となります。
$$t_{1}=\frac{L}{C+v\rm{cos}θ}・・・(3)$$
$$t_{2}=\frac{L}{C-v\rm{cos}θ}・・・(4)$$
ただし、音速Cは流体の温度や組成変化の影響を受けるので、(3)、(4)式中に含まれているのは好ましくありません。
そこで式変形により音速Cを消去します。
周波数の差Δfをt1、t2から求めます。
$$Δf=f_{1}-f_{2}=\frac{1}{t_{1}}-\frac{1}{t_{2}}=\frac{2v\rm{cos}θ}{L}$$
$$v=\frac{L}{2\rm{cos}θ}(\frac{1}{t_{1}}-\frac{1}{t_{2}})・・・(5)$$
(5)式のように、流体の流速vが音速Cによる影響を受けず、伝播時間の差から求めることができます。
また、流量Qは流速vに配管断面積Aをかけて算出できます。
ドップラー方式
流体中の気泡や固形物に超音波を照射し、送信波と受信波の周波数の差から流速及び流量を計算する方式です。
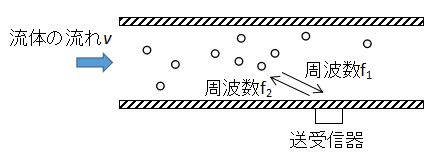
ドップラー効果によって反射する超音波は周波数がシフトすることを利用しています。
原理的に、流体中に超音波が反射するような物質(気泡や固形物)がないと測定できません。
超音波式流量計の特徴
- 圧力損失を生じない。
- 管外から後付けで測定可能(クランプオン型)。
- 大口径管(~7,000A程度)に適用可能で、大口径になるほど他の流量計より相対的に安価。
- 正逆流の測定が可能。
- 本質的に流速計であるため、流速分布の影響を受ける。
- 測定原理によって固形物や気泡が含まれる場合の測定可否が変わる。
- 伝播速度差方式:固形物や気泡が多く含まれる(2~5%以上)と測定できない。
- ドップラー方式:固形物や気泡が液中にないと測定できない。
伝播経路数
超音波流量計での測定にはある程度の伝達経路長が必要です。
前述した図では対角に設置していますが、場合によっては設置方法を変更する必要があります。
以下の表によく使用される伝播経路数(Sound Path)を示します。
| 伝播経路数 | 信号伝播経路 |
| 1 | 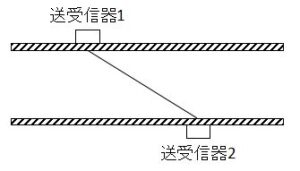 |
| 2 | 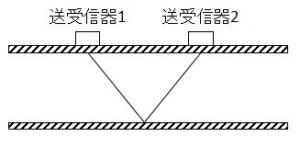 |
| 3 | 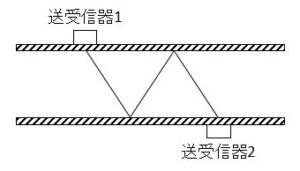 |
| 4 | 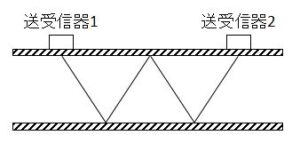 |
大口径ではSound Path 1、中口径ではSound Path 2を使用します。
小口径になると取り付ける検出器同士の間隔が狭くなるため、Sound Path 2では物理的に取り付けられないことがあります。
そのような場合は、Sound Path 3やSound Path 4を使用します。
まとめ
超音波式流量計について解説しました。
クランプオン型の超音波流量計は他の流量計にはないメリットがありますので、使用する機会も多いと思います。
