概要
熱力学第一法則は仕事と熱を含めたエネルギー保存則を示していました。
しかしエネルギー保存則を満たしていれば、どのような現象も自由に起こり得る、ということではありません。
例えば、
- 沸騰させたお湯を放置しておくとかならず冷める。逆に常温の水を放置しても沸騰することはない。
- コーヒーにミルクを入れてスプーンで混ぜると均一になる。逆にどれだけスプーンを巧みに動かしても、均一となったコーヒーからミルクだけを分離することはできない。
以上のような現象の不可逆性を私たちは経験的に知っています。
このように、世の中の現象(あるいはエネルギー変化)が起こり得る方向性が決まっていることを表した法則を熱力学第二法則といいます。
熱力学第二法則の表現
熱力学の第二法則は1つの定義で決まっているわけではなく、様々な人が提唱した原理から成っています。
ただしそれぞれの原理は全て同値であり、本質的には同じことを言っています。
この記事ではいくつかの原理について紹介します。
クラウジウスの原理
クラウジウスの原理は、"他に何の変化も残さずに、熱を低温の物体から高温の物体に移すことはできない"、ということを示した原理です。
前述した"常温の水を放置しても沸騰することはない"、というのはまさにクラウジウスの原理をよく表していますね。
例えば低温から高温へと熱を移動させる手法としては、エアコンや冷凍機で使用されているヒートポンプが挙げられます。
しかしヒートポンプを駆動するには動力が必要で、"他に何の変化も残さずに"熱を移動させているわけではありません。
そのため、ヒートポンプはクラウジウスの原理に反していません。
トムソンの原理
トムソンの原理は、"他に何の変化も残さずに、ただ1つの熱源から熱を取り出しそれをすべて仕事に変え、自身は元の状態に戻ることはできない"、ということを示した原理です。
熱力学の第一法則から言えば熱と仕事は同じエネルギーなので、熱を仕事に100%すべて変えることができそうではあります。
このような熱を仕事へと100%変換できる装置を第二種の永久機関といいます。
実際には熱を仕事へ100%変換することは不可能で、第二種の永久機関は実現できません。
実現可能な熱機関では、
- 熱から仕事を取り出せる効率(熱効率)が存在する。
- 仕事として取り出せなかった熱は低熱源に捨てる必要がある。
少なくとも以上の条件を満たす必要があります。
クラウジウスの不等式
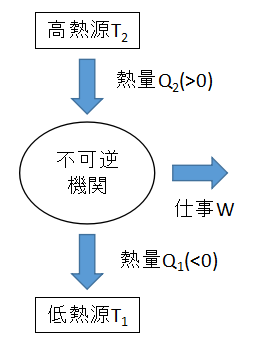
上図のように、温度T2の高熱源から熱量Q2を受け取り、その一部を仕事に変え、残りの熱量Q1を温度T1の低熱源に捨てる不可逆機関を考えます。
この不可逆機関の熱効率η'は、
$$η'=1+\frac{Q_{1}}{Q_{2}}・・・(1)$$
(1)式となります。
一方で、同じ高熱源、低熱源を利用した最大効率の可逆機関(カルノーサイクル)の熱効率ηは、
$$η=1-\frac{T_{1}}{T_{2}}・・・(2)$$
(2)式となります。
これらの熱効率の間には、
$$η'≦η・・・(3)$$
(3)式の関係が成立します。
(1)、(2)式を(3)式に代入して整理すると、
$$\frac{Q_{1}}{T_{1}}+\frac{Q_{2}}{T_{2}}≦0・・・(4)$$
(4)式となります。
仮に熱機関が可逆機関であれば、(4)式は等号となりますし、不可逆機関であれば不等号が成り立ちます。
また、(4)式は2つの熱源との熱のやり取りから導出されましたが、もっと細かくより多くの熱源と熱のやり取りを行なうことを考えます。
熱源の数を無限に増やしていくと、(4)式は最終的に積分系となります。
$$\int_{C}\frac{δQ}{T}≦0・・・(5)$$
(5)式は熱機関のサイクルが1巡したときのδQ/Tの値がゼロ以下になることを示しています。
この(5)式をクラウジウスの不等式といいます。
エントロピー増大の法則
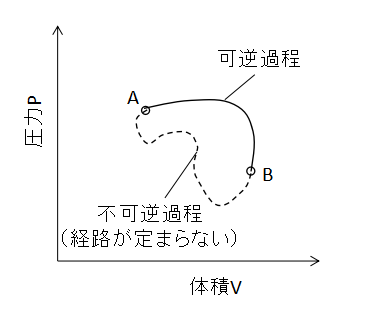
上図のように、可逆過程と不可逆過程からなるサイクルを考えます。
(5)式を可逆過程と不可逆過程それぞれに対して適用すると、
$$\int_{C}\frac{δQ}{T}=\int_{A(Cr)}^{B}\frac{δQ}{T}+\int_{B(Cn)}^{A}\frac{δQ}{T}≦0・・・(6)$$
(6)式となります。
ここで、エントロピーの定義から、
$$S_{B}-S_{A}=\int_{A(Cr)}^{B}\frac{δQ}{T}・・・(7)$$
(7)式が成り立ちます。(7)式を(6)式に代入すると、
$$S_{A}-S_{B}≧\int_{B(Cn)}^{A}\frac{δQ}{T}・・・(8)$$
(8)式となります。
(8)式を微分形式で表すと、
$$dS≧\frac{δQ}{T}・・・(9)$$
(9)式となります。
ここで、この不可逆変化が断熱変化とすると、δQ=0となるため、
$$dS≧0・・・(10)$$
(10)式となります。
したがって、外部と断熱され孤立した系において、不可逆変化が起こった場合はエントロピーが必ず増大することになります。
これをエントロピー増大の法則といいます。
一方で、外部と熱のやり取りがある場合には、対象としている系のエントロピーが減少することもあるので注意しましょう。
おわりに
熱力学第二法則について解説しました。
熱力学の第一法則と並んで重要な法則です。エントロピーと合わせて覚えておきましょう。
