概要
スプライン(Spline)補間はあるデータを多項式で補間する手法の1つです。
データの点で区間を区切り、区間ごとに異なる多項式を使用して補間する手法です。
ラグランジュ補間でRunge現象が発生し振動するようなデータでも滑らかに補間することが可能です。
本記事ではPythonを使用した簡単なスプライン補間法を紹介します。
スプライン補間式
ここではよく使用される3次スプラインを解説します。
原理
例として(x0,y0) 、(x1,y1)、(x2,y2)の3個のデータをスプライン補間することを考えます。
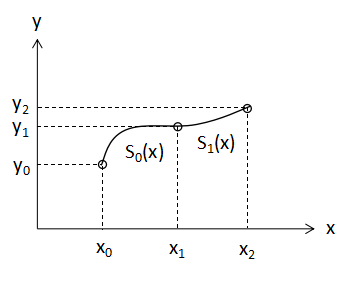
補間のイメージを上図に示します。区間[x0,x1]は多項式S0(x)で補間し、区間[x1,x2]は多項式S1(x)で補間します。
このとき、多項式S0(x) 、S1(x)は
$$S_{0}(x)=a_{00}x^{3}+a_{01}x^{2}+a_{02}x+a_{03}・・・(1)$$
$$S_{1}(x)=a_{10}x^{3}+a_{11}x^{2}+a_{12}x+a_{13}・・・(2)$$
(1),(2)式のように3次の多項式で表します。
1つの多項式につき未知数が4つありますから、合計で8つの未知数があります。
後は制約条件等によって未知数を算出する8つの式を立てるだけです。
まずは多項式が通る点について考えましょう。
多項式S0(x)は点(x0,y0) 、(x1,y1)を通り、多項式S1(x)は (x1,y1)、(x2,y2)を通ります。したがって、
$$S_{0}(x_{0})=y_{0}・・・(3)$$
$$S_{0}(x_{1})=y_{1}・・・(4)$$
$$S_{1}(x_{1})=y_{1}・・・(5)$$
$$S_{1}(x_{2})=y_{2}・・・(6)$$
(3),(4),(5),(6)式が成り立ちます。
次に多項式同士の接続について考えます。
S0(x)とS1(x)が滑らかに接続されるためには、接続点である点(x1,y1) で一次微分、二次微分が一致している必要があります。したがって、
$$S'_{0}(x_{1})=S'_{1}(x_{1})・・・(7)$$
$$S''_{0}(x_{1})=S''_{1}(x_{1})・・・(8)$$
(7),(8)式が成り立ちます。
最後に自然スプラインの条件として、端点での二次微分がゼロとします。
$$S''_{0}(x_{0})=0・・・(9)$$
$$S''_{1}(x_{2})=0・・・(10)$$
これで(3)~(10)式の合わせて8つの式が立ちましたので、(1),(2)式の未知数8つを求めることができます。
一連の流れを一般化してみます。
(x0,y0) 、(x1,y1)・・・(xn,yn)のn+1個のデータをスプライン補間すると考えます。
多項式Sj(x)は
$$S_{j}(x)=a_{j0}x^{3}+a_{j1}x^{2}+a_{j2}x+a_{j3}・・・(11)$$
(11)式として与えられます(j=0,1,・・・n-1)。多項式の数はS0(x)からSn-1(x)までn個あります。
未知数の数は多項式1つにつき4つあるので、合計で4n個あります。
次に制約条件式についてです。
まず多項式が通る点は、1つの多項式につき2つあります。多項式Sj(x)について式を立てると
$$S_{j}(x_{j})=y_{j}・・・(12)$$
$$S_{j}(x_{j+1})=y_{j+1}・・・(13)$$
(12),(13)式となります。多項式はn個あるので(12),(13)式は合計で2n個の式となります。
次に一次微分、二次微分についても同様に式を立てます。
$$S'_{j}(x_{j})=S'_{J+1}(x_{j})・・・(14)$$
$$S''_{j}(x_{j})=S''_{j+1}(x_{j})・・・(15)$$
(14),(15)式となります。多項式の接続点はn+1個の点から端点2個を引いたn-1個となりますので、(14),(15)式は合計で2n-2個の式となります。
最後に端点で二次微分がゼロとなる条件を考えると、
$$S''_{0}(x_{0})=0・・・(16)$$
$$S''_{n-1}(x_{n})=0・・・(17)$$
(16),(17)式となります。
したがって、条件式の数は2n+(2n-2)+2=4n個となり、未知数の数4nと等しくなったので解くことができます。
ただしデータの個数が多い場合には方程式の数が多くなるのでExcelでは大変ですね。
Pythonにはスプライン補間を簡単に解くことができるモジュールが用意されているので今回はそれを紹介します。
Pythonでの計算法
計算条件
ラグランジュ補間の解説記事でRunge現象を起こしていたデータをスプライン補間してみましょう。

データは
| x | y |
| 1.0 | 14.1 |
| 2.0 | 16.5 |
| 3.0 | 22.9 |
| 5.0 | 31.3 |
| 10.0 | 46.0 |
| 12.0 | 44.8 |
| 20.0 | 63.2 |
上の7点です。
比較の為にラグランジュ補間もScipyを使って計算し、グラフに載せます。
ライブラリ・モジュールのインポート
スプライン補間とラグランジュ補間の関数を使用するためにScipyをインポートします。
また、補間時に必要なxの値を作成するためにNumpyの関数が便利なのでインポートします。
加えてPythonでグラフを作成しますのでMatplotlibをインポートします。
#モジュールインポート
from scipy.interpolate import lagrange
import scipy.interpolate as scipl
import numpy as np
import matplotlib.pyplot as plt前提条件の入力
前提条件としてデータをリストにして入力します。
#前提条件
x_lis=[1,2,3,5,10,12,20]
y_lis=[14.1,16.5,22.9,31.3,46,44.8,63.2]補間式計算
補間計算に必要な情報を入力しています。
#補間式
x=np.arange(1,21,0.1)
f_lag=lagrange(x_lis,y_lis) #ラグランジュ補間
f_sci=scipl.CubicSpline(x_lis,y_lis) #スプライン補間まず2行目で補間計算時の横軸xの範囲と刻み幅を指定しています。括弧内は(開始値,終了値,刻み幅)です。x=1~21まで0.1刻みとしました。
3行目でラグランジュ補間を計算しています。lagrange関数を使用することで簡単にラグランジュ補間を計算できます。括弧内は補完するデータのxとyのリストを入力します。
4行目でスプライン補間を計算しています。CubicSpline関数を使用することで3次スプライン補間を計算できます。
グラフの出力
最後にグラフの出力設定をします。
#グラフ出力
plt.plot(x_lis, y_lis,'o')
plt.plot(x, f_lag(x),'-')
plt.plot(x, f_sci(x),'-')
plt.xlabel('x [-]')
plt.ylabel('y [-]')
plt.legend(['Row data','Lagrange','Cubic Spline'])
plt.show()計算結果の確認
特に入力ミス等がなければグラフが以下のように表示されます。
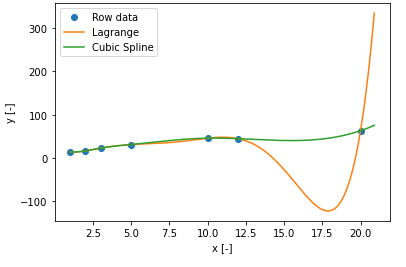
ラグランジュ補間が大きく振動しているのに対して、スプライン補間は滑らかに補間できていますね。
最後に全体のコードを載せておきます。
#モジュールインポート
from scipy.interpolate import lagrange
import scipy.interpolate as scipl
import numpy as np
import matplotlib.pyplot as plt
#前提条件
x_lis=[1,2,3,5,10,12,20]
y_lis=[14.1,16.5,22.9,31.3,46,44.8,63.2]
#補間式
x=np.arange(1,21,0.1)
f_lag=lagrange(x_lis,y_lis) #ラグランジュ補間
f_sci=scipl.CubicSpline(x_lis,y_lis) #スプライン補間
#グラフ出力
plt.plot(x_lis, y_lis,'o')
plt.plot(x, f_lag(x),'-')
plt.plot(x, f_sci(x),'-')
plt.xlabel('x [-]')
plt.ylabel('y [-]')
plt.legend(['Row data','Lagrange','Cubic Spline'])
plt.show()まとめ
補間手法の基礎であるスプライン補間法について解説しました。
ラグランジュ補間でうまく補間出来ない場合は、スプライン補間を試してみるのがよいでしょう。
