概要
現実の流体は粘性を持っており、流体が動くときには相互運動を妨げる方向に力が働きます。
この力が流体の速度分布に比例する法則のことをニュートンの粘性法則といいます。
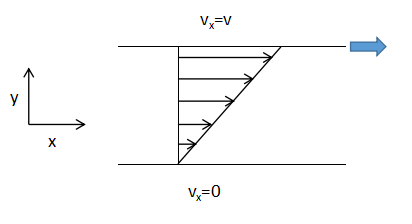
上図のような平板間の流体の流動を考えます。
上の平板は速度vでx軸方向に動いており、下の平板は静止しているとします。
このときの平板間の流体の速度分布は上図のようになります。
これは速度vで動く平板に引きずられて流体が動いたために起こる現象です。
流体には平板が動くのを妨げようとして摩擦によるせん断応力が働き、このせん断応力によって流体も平板につられて動きます。
このとき、流体に働くせん断応力τyxは(1)式のように表されます。
$$τ_{yx}=-μ\frac{dv_{x}}{dy}・・・(1)$$
もしくは材料力学では(2)式のような形で表されます。
$$τ=μ\dot{γ}・・・(2)$$
τyx:せん断応力[Pa]、μ:流体粘度[Pa・s]
vx:x方向の流体の流速[m/s]、y:y方向の位置[m]
γ:流体のせん断速度の時間微分[1/s]
(1)式は粘性流体の流動を考えるうえで非常に重要な式で、ハーゲン・ポアズイユの式やナビエ・ストークス式の導出などにも出てきます。
流体の流速を計算するうえでの基本的な式なので覚えておくとよいでしょう。
ニュートン流体について
(1),(2)式のように流体に働くせん断応力と流体の速度勾配の間に比例関係が成立する流体のことをニュートン流体といいます。
ニュートン流体の場合、温度一定であれば流体の流速によらず粘度が一定値を示します。
水や空気、グリセリンなどの分子構造が簡単な物質であればニュートン流体とみなせます。
一方で高分子溶液など分子構造が複雑な流体や固体粒子が分散したスラリー液はニュートンの粘性法則(1),(2)式に従わない非ニュートン流体であることが多いので、もし取り扱うことがあれば注意が必要です。
非ニュートン流体について
非ニュートン流体のモデル化
非ニュートン流体は流体に働くせん断応力と流体の速度勾配の間に比例関係が成立せず、流体の流速によって粘度が変化する流体です。
もし実務で非ニュートン流体の流動状態を正確に計算する必要がある場合には、ニュートンの粘性法則である(1),(2)式を非ニュートン流体に適用できるよう修正した式を使用します。
非ニュートン流体の修正式は様々ありますが、最も汎用的に使用できるモデルは(3)式のHershcel-Bulkeyモデルだと思います。
$$τ=τy+K\dot{γ}^{n}・・・(3)$$
τ:非ニュートン流体にかかるせん断応力[Pa]
τy:非ニュートン流体の降伏応力[Pa]
K:係数、n:指数
非ニュートン流体の種類によって降伏応力τy、係数K、指数nの値が変わってきます。
これら3つのパラメータは文献等から情報が得られることはほとんどなく、実物の溶液を作成し粘度測定をしてパラメータを得るのが現実的な手法です。
ただ、実際の実務では熱流体計算をするグループと実験してデータを取るグループは異なると思いますし、社内に粘度測定のノウハウがなければ社外に依頼することになるでしょう。
そのため非ニュートン流体の粘度測定はやろうとするとかなり面倒くさく時間もかかります。
したがって、弊社では非ニュートン流体であってもニュートン流体として熱流体計算することが多いです。
解析対象の装置によりますが、例えば撹拌槽では粘度が変化することを見込んで、最も粘度が高くなる条件で計算し混合状態を担保しておけば問題ないことがほとんどです。
非ニュートン流体の種類
塑性流体
降伏応力τyを持つ流体のことを塑性流体といいます。
塑性流体は流体にかかるせん断応力が、ある降伏応力を超えないと流動せず固体のような性質を示します。
印刷インキ、血液、アスファルト、歯磨き粉などがこの塑性流体に当てはまります。
ビンガム流体
塑性流体の中でもある種の理想的な振る舞いをする流体をビンガム流体といいます。
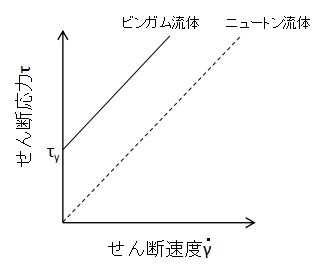
上図にビンガム流体とニュートン流体の比較を示します。
縦軸が流体にかかるせん断応力で、横軸がせん断速度の時間微分γです。
塑性流体は降伏応力を持つため、γ=0でもτ=0とならないのが特徴です。
なおかつビンガム流体はいったん流動し始めると粘度ηは一定値を示すことから、(3)式においてK=η、n=1となるため、
$$τ=τy+η\dot{γ}・・・(4)$$
(4)式のように簡略化して表すことができます。
非ビンガム流体
ビンガム流体のように粘度が一定値を示さない流体を非ビンガム流体といいます。
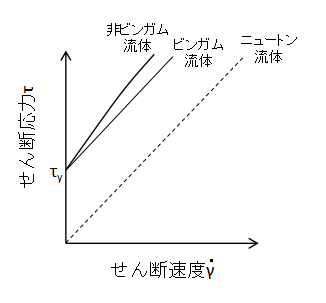
上図に非ビンガム流体とニュートン流体の比較を示します。
非ビンガム流体はいったん流動し始めてからも粘度ηは流速により変化するため、曲線で表されます。
ビンガム流体のように(3)式を簡略化することはできません。
擬塑性流体
指数n<1となる流体を擬塑性流体といいます。
擬塑性流体はせん断速度が低いうちは高い粘度を示しますが、せん断速度が高くなるにつれ粘度が減少して最終的には一定値を示すような性質を持ちます。
せん断速度が低いときは分子同士が二次的な結合をしており流動しにくいため粘度が高くなりますが、せん断速度が高くなると二次的な結合が物理的に切られるため流動しやすくなり粘度が低くなります。
高分子を含む溶液は分子鎖が長く二次的な結合をしやすいため擬塑性流体であることが多いです。
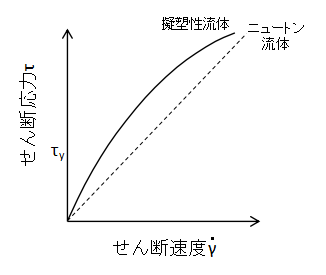
上図に擬塑性流体とニュートン流体の比較を示します。
擬塑性流体は原点を通り、上に凸の曲線となります。
降伏応力は持たないため、τy=0とすることができます。したがって(3)式は、
$$τ=K\dot{γ}^{n}・・・(5)$$
$$n<1$$
(5)式のように簡略化することができます。
ダイラタント流体
指数n>1となる流体をダイラタント流体といいます。
ダイラタント流体は静置している状態では最密充填にある構造が、外力を加えることで最密充填ではなくなり、分散媒である液体が不足し粒子同士が直接接することで固体のような挙動を示します。
したがって、せん断力が低いうちは粘度は低い値を示しますが、せん断力が高くなると高い粘度を示すようになります。
高濃度の粒子が分散しており、粒子径がそろっている溶液はダイラタンシー性を示すことがあります。
身近な例では水溶き片栗粉がダイラタンシー性を示します。
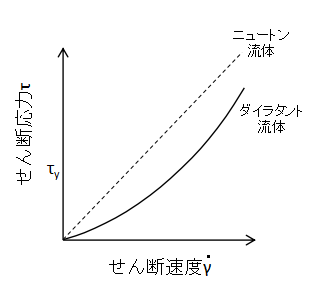
上図にダイラタント流体とニュートン流体の比較を示します。
ダイラタント流体は原点を通り、下に凸の曲線となります。
降伏応力は持たないため、τy=0とすることができます。したがって(3)式は、
$$τ=K\dot{γ}^{n}・・・(5)$$
$$n>1$$
(5)式のように簡略化することができます。
