概要
液液撹拌は乳化重合や液液抽出など、界面を通しての物質移動が重要になる系で行なわれる操作です。
撹拌翼によるせん断により小さな液滴を発生させることで界面積が増加し、物質移動が促進されます。
液液撹拌は混合する液の特性によって、
- 均一系撹拌:相互溶解する
- 異相系撹拌:相互溶解しない
2種類に分類されますが、一般に液液撹拌というと異相系撹拌を指すことが多いです。
異相系撹拌は撹拌条件によって液滴の分散状態や物質移動が影響を受けやすく、適切な運転条件を設定するには撹拌の知識が必要となります。
本記事では液液撹拌における分散状態や液滴径制御について解説しています。
液滴の分散状態の変化
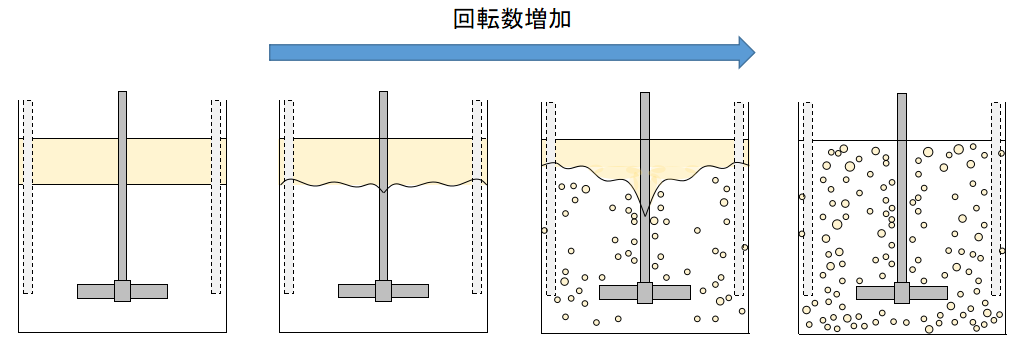
撹拌槽内に水と油のような互いに溶け合わない液体を投入した場合、撹拌回転数によって液液分散の状態が大きく変化します。
ここでは水よりも比重の軽い油と水の液液分散について考えてみます。
液液分散状態は撹拌回転数を増加させていくと、以下の4つのような分散状態に変化していきます。
静止状態
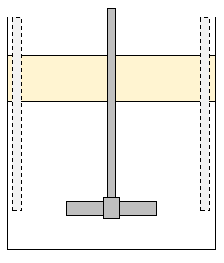
撹拌翼が停止していると、水と油は完全に2相に分離します。
この状態は水-油間の物質移動速度が遅く、かつ濃度分布が極端に発生しています。
反応系の場合は副反応や発熱を避けるため、撹拌翼が停止した状態はなるべく短くすべきでしょう。
また、撹拌後に上澄み液のみを取得する場合には、十分な時間静置する必要があります。
ストークスの式を使用することで液滴の分離時間を大まかに予測できますが、最終的には実際にやってみて静置時間を調整する必要があります。
液液界面の揺らぎ
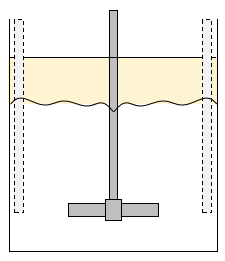
少し回転数が増加すると、水相のみに循環流が発生します。
液液界面は循環流の影響で揺らぎ始めます。しかし、水と油の物質移動は静止状態のときとほとんど変わらず遅いままです。
この状態で運転する理由はないので、さらに回転数を上げるべきです。
油相液滴の生成・分散
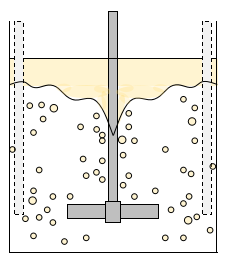
さらに回転数が増加すると、油相の一部が循環流によって水相に引き込まれ、油相液滴が生成・分散します。
油滴の大きさは撹拌翼のサイズや回転数、油滴の物性に依存します。
回転数が大きくなるにつれて油相の厚みは薄くなっていき、分散している油滴が増加します。
完全分散状態
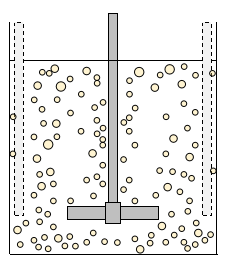
さらに回転数が増加すると、完全に油相がなくなり油滴として分散した状態となります。
この状態を完全分散状態といい、このときの回転数を完全分散限界翼速度ncといいます。
汎用の撹拌翼では完全分散限界翼速度ncを推算することができます。
$$\frac{{n_{c}}^{2}ρ_{m}d}{gΔρ}=C_{2}(\frac{D}{d})^{2α}φ^{0.106}(\frac{{μ_{m}}^{2}σ}{d^{5}ρ_{m}g^{2}Δρ^{2}})^{0.084}・・・(1)$$
$$ρ_{m}=φρ_{d}+(1-φ)ρ_{c}・・・(2)$$
$$μ_{m}=\frac{μ_{c}}{1-φ}(\frac{1.5μ_{d}φ}{μ_{d}+μ_{c}})・・・(3)$$
"ミキシング技術の基礎と応用"より引用
Δρ:連続相と分散相の密度差、μc:連続相密度、μd:分散相密度、φ:分散相体積分率
D:槽径、d:翼径、C2,α:幾何形状に関するパラメータ
幾何形状に関するパラメータは以下の表に示す値が報告されています。
| 翼種 | 翼枚数 | 液深H/槽径D | 翼の取付位置 | C2 | α |
| プロペラ翼 | 3 3 3 3 | 1 1 1 1 | (1/4)H (3/4)H (1/2)H (1/4)H、(3/4)H | 4.38 2.76 4.33 1.46 | 0.67 0.95 0.79 1.33 |
| 傾斜タービン翼 | 6 6 6 6 | 1 1 1 1 | (1/4)H (3/4)H (1/2)H (1/4)H、(3/4)H | 1.95 1.96 0.84 0.94 | 1.44 1.17 1.97 1.27 |
| タービン翼 | 6 6 6 6 | 1 1 1/2 3/2 | (1/4)H (1/2)H (1/2)H (1/2)H | 0.91 0.95 0.70 1.10 | 2.02 1.38 1.24 1.70 |
| ディスクタービン翼 | 6 | 1 | (1/2)H | 0.53 | 1.70 |
"ミキシング技術の基礎と応用"より引用
ラボ実験で目視で液滴の分散状態を確認できるならば、ncをわざわざ推算する必要はないかもしれません。
しかし実機の撹拌槽は槽内の分散状態を確認することが難しいので、推算式でncを算出しておくことは有用です。
スケールアップ時の液滴径制御
撹拌槽をラボから実機へとスケールアップする際に、撹拌によって生成する液滴径をコントロールしたい、という要望があるかと思います。
ここでは乱流条件下においてスケールアップする際の有効な指標について解説します。
$$N_{p}=\frac{P}{ρn^3d^5}・・・(4)$$
P:動力[W]、ρ:液体密度[kg/m3]、n:回転数[1/s]、d:翼径[m]
(4)式で定義されます。乱流条件下ではNp=一定となるため、
$$P∝n^3d^5・・・(5)$$
(5)式が成立します。
次に液体積をVとすると、幾何学的相似条件下では、
$$V∝d^3・・・(6)$$
(6)式が成立します。
単位体積当たりの動力Pvについて、(5),(6)式から、
$$P_{v}=\frac{P}{V}∝n^3d^2・・・(7)$$
(7)式となります。
また、一方で撹拌We数と液滴の体面積平均径d32の関係はこちらの記事で詳しく解説していますが、
$$\frac{d_{32}}{d}=C・We^{-\frac{3}{5}}・・・(8)$$
d32:体面積平均の液滴径[m]、C:定数
(8)式となります。
(8)式を回転数n、翼径dについて整理すると、
$$d_{32}=C・d・(\frac{ρn^2d^3}{σ})^{-\frac{3}{5}}∝(n^3d^2)^{-\frac{2}{5}}∝(P_{v})^{-\frac{2}{5}}・・・(9)$$
(9)式となります。
したがって、体面積平均径d32は単位体積当たりの動力Pvに比例することがわかります。
そのため、撹拌槽をPv一定でスケールアップすると、体面積平均径d32を一定とできます。
一般に撹拌槽はPv一定でスケールアップすることが多いため、スケールアップ時に設定しやすい条件だと言えるでしょう。
ただし注意点として、
- 複数の仮定をおいている。
- 乱流条件下
- スケールアップ前後で幾何学相似
- 液物性(密度、粘度、表面張力)が同等
- あくまで液滴の平均径が一定となる。(液滴径分布まで一定とはならない。)
以上のような事項が挙げられます。
特に幾何学相似については完全に順守するのが難しいこともあります。ラボで実験する段階から、なるべく実機形状に近いような装置でデータを取得することをオススメします。
おわりに
液液撹拌について解説しました。
Pv一定でスケールアップすれば液滴径を一定とすることができます。撹拌の目的に応じて回転数・動力を設定しましょう。
