概要
同一物質内、あるいは密接した物体間に温度差がある場合、物質の移動を伴わない熱エネルギーのみの移動現象が発生します。
この現象を伝導伝熱といい、伝導伝熱における伝熱量の関係をフーリエの法則といいます。
$$q=-k\frac{dT}{dx}・・・(1)$$
q:熱流束[W/m2]、k:熱伝導度[W/(m・K)]
T:温度[K]、x:物質の厚み[m]
フーリエの法則は(1)式で表されます。
伝導伝熱はほとんどあらゆる状況において発生しているという点で、非常に重要な伝熱形態です。
ただし、対流伝熱等と比較して熱が伝わりにくい形態でもあります。
熱の伝わりやすさは物質の種類によりますので、材質選定の際には気を付けましょう。
特に耐食性を考慮して金属からライニング材に変更する場合には伝熱が悪くなるため、事前に伝熱計算して運転に支障がないか確認すべきです。
様々な物質の熱伝導度
伝導伝熱の計算に必要な熱伝導度は、物質によって値がかなり異なります。
代表的な物質の300K、101.3kPaにおける熱伝導度を下の表に示します。
| 物質 | 熱伝導度k [W/(m・K)] | 物質 | 熱伝導度k [W/(m・K)] |
| 水素 | 0.181 | アルミニウム | 237 |
| ヘリウム | 0.153 | マグネシウム | 156 |
| メタン | 0.034 | ニッケル | 90.5 |
| 空気 | 0.026 | 鉄 | 80.3 |
| 二酸化炭素 | 0.017 | 白金 | 71.4 |
| 水銀 | 8.52 | 鉛 | 35.2 |
| 水 | 0.610 | チタン | 21.9 |
| アンモニア | 0.479 | 黄銅(Cu-40Z) | 123 |
| エチレングリコール | 0.258 | はんだ | 46.5 |
| メタノール | 0.208 | 炭素鋼(S35C) | 43.0 |
| 潤滑油 | 0.086 | ステンレス鋼(SUS304) | 16.0 |
| 銀 | 427 | チタン合金(Ti-6Al-4V) | 7.60 |
| 銅 | 398 | サファイア | 46.0 |
| 金 | 315 | 石英ガラス | 1.38 |
| ソーダガラス | 1.03 | ||
| アクリル樹脂 | 0.21 |
金属が最も熱伝導度が高い傾向にあります。実体験から考えても納得のいく傾向ですね。
物質の状態では大まかに、
固体の熱伝導度>液体の熱伝導度>気体の熱伝導度
の傾向があります。
例えば断熱材は、構造の中に熱伝導度の低い気体を含むことで熱が周囲に伝わりにくいようにしています。
実務で熱伝導度が必要なときは文献やデータベース等を調べるか、値が載っていなければ推算することもあります。
以下の記事で熱伝導度の推算方法を解説しています。
-

【熱伝導度】推算方法を解説:フーリエの法則の比例定数
気体や液体の熱伝導度は主に熱流体解析をするうえで必要になってきます。熱伝導度はフーリエの法則で使用されているため、伝導伝熱の寄与に関係します。
続きを見る
伝導伝熱と対流伝熱の大小
実務でANSYS等の汎用の熱流体解析ソフトで計算する場合には、伝導伝熱計算はデフォルトで計算するよう設定されていると思いますのであまり気にする必要はありません。
ただし、エクセル等で自分で式を立てて計算する場合は、伝導伝熱を考慮する必要があるかどうか考えなければなりません。
ここでは配管流れの伝熱を例として伝導伝熱の寄与を確認してみます。
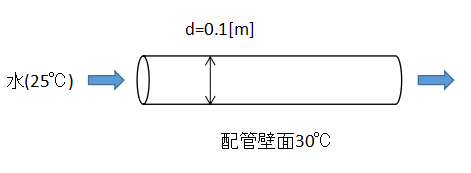
上図に示すような配管流れを考えます。
25℃の水を配管内に流し、壁面30℃で中の流体を加熱します。
このとき、配管内の流体は伝導伝熱と対流伝熱により加熱されるとして、それぞれの熱流束を計算します。
(輻射伝熱は無視します。)
使用する水の物性について、本来なら温度依存がありますが簡単のため25℃のときの値を使用します。
・密度:997kg/m3
・粘度:0.00089Pa・s
・比熱:4182.8J/(kg・K)
・熱伝導度:0.606W/(m・K)
配管内径は0.1mとします。
伝導伝熱計算
壁面(30℃)から配管中心(25℃)までの伝導伝熱の熱流束は(1)式から、
$$q=0.606×=\frac{30-25}{0.05}=61W/m^{2}$$
となります。
(壁面から流体への熱流束を正とします。)
後に計算する対流伝熱の熱流束と比較してみましょう。
対流伝熱計算
対流伝熱はニュートンの冷却法則から計算できます。
ただし、流れの状態により境膜伝熱係数が変化するため、乱流と層流の場合でそれぞれ計算してみます。
ちなみに、配管内流れの境膜伝熱係数の計算式は下の記事で解説しています。
-

熱交換器【管内側境膜伝熱係数】を解説:チューブ内流れの伝熱
この記事では配管や熱交換器の伝熱管内を流れる流体の境膜伝熱係数についてまとめています。配管内の流動は他の流れに比べると単純で、種々の相関式が発表されています。
続きを見る
乱流
配管内の断面平均流速を1m/sとすると、レイノルズ数Re=112,000となり乱流になります。
このときの境膜伝熱係数はコルバーンの実験式から計算してみます。
$$Nu=0.023×112000^{0.8}×6.14^{0.4}≒520$$
$$h=\frac{520×0.606}{0.1}≒3150$$
$$q=3150×(30-25)≒15750W/m^{2}$$
となります。
伝導伝熱の61W/m2と比較すると、ものすごく大きな値となりました。
全体の熱流束のうち、伝導伝熱の寄与率は0.4%程度の大きさです。
したがって、乱流流れの場合は伝導伝熱はほとんど無視しても問題ないと言えます。
層流
配管内の断面平均流速を0.01m/sとすると、レイノルズ数Re=1,120となり層流になります。
このときの境膜伝熱係数はSiederの式から計算してみます。
$$Nu=4×6.14^{1/3}×1^{0.14}≒7.3$$
$$h=\frac{7.3×0.606}{0.1}≒44$$
$$q=44×(30-25)≒222W/m^{2}$$
となります。
伝導伝熱の61W/m2よりは大きな値となりましたが、乱流ほどではありません。
全体の熱流束のうち、伝導伝熱の寄与率は21.6%程度の大きさです。
伝導伝熱の寄与率が20%もあればさすがに無視するわけにはいきません。
したがって、層流流れの場合は伝導伝熱を考慮する必要があると言えます。
まとめ
伝導伝熱の基礎式であるフーリエの法則について解説しました。
一般的にプラント内の流体は乱流状態であることが多いため、伝導伝熱の影響は小さいです。
しかし流体の熱物性や流速によっては伝導伝熱の寄与が大きいこともありますので注意が必要です。

