【圧縮係数（圧縮率因子）】を解説：非理想性を表わす指標

概要

実在気体と理想気体のズレを表わす指標を圧縮係数z（もしくは圧縮率因子）と言います。

$$z=\frac{V_{real}}{V_{ideal}}=\frac{PV}{RT}$$

z：圧縮係数[-]、V_real：実在気体の体積[m³/mol]、V_ideal：理想気体の体積[m³/mol]
P：圧力[Pa]、T：温度[K]、R：気体定数[Pa・m³/(mol・K)]

圧縮係数zは上式のように理想気体の状態方程式の係数として表されます。
理想気体の場合は常にz=1となりますが、実在気体の場合は様々な値を取ります。

とはいえ低圧条件下では圧縮係数zは1に近い値を示し、実在気体が理想気体に近い挙動を示すことが知られています。

逆に臨界点付近はzが1を大きく下回り非理想的な挙動を示すため、ちゃんと非理想性を考慮したモデルで推算しなければなりません。

化学工学的には圧縮因子zを利用して気体密度の推算を簡単に行うことができます。

一般化圧縮係数線図による気体密度推算

対応状態原理に従う物質は種類に関係なく同一の対臨界定数で表すことができます。

したがって圧縮係数に関しても概要の式を対臨界状態に適用すれば、

$$z=\frac{P_{r}V_{r}}{RT_{r}}$$

T_r：対臨界温度[-]、P_r：対臨界圧力[-]、V_r：対臨界体積[-]

となり、同一の対臨界定数となれば同一の圧縮係数となることがわかります。

この関係を線図化したものが一般化圧縮係数線図と呼ばれており、下に示します。

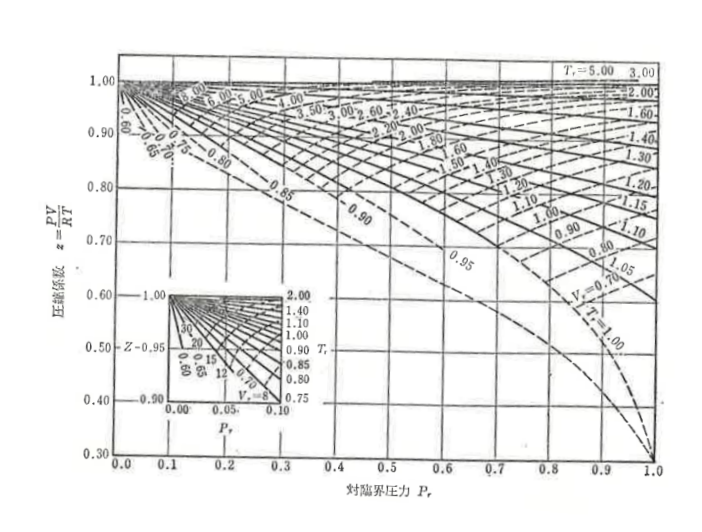
上表は縦軸に圧縮係数z、横軸に対臨界圧力P_rを取ったものです。
この表は横軸のレンジがP_r=1.0までですが、P_rがもっと大きい値を取るとき用の線図もあります。

対臨界定数のうち2定数を算出すればこの表から圧縮因子zを読み取ることができます。
その後は

$$z=\frac{PV}{RT}$$

$$ρ=\frac{M}{V}$$

ρ：密度[kg/m³]、M：分子量[kg/mol]

上の2式の関係から

$$ρ=\frac{MP}{zRT}$$

この式を導出し使用すれば気体の密度を求めることができます。