概要
流体に関するエネルギー保存則のことを特にベルヌーイの定理といいます。
圧縮性と粘性のない完全流体のベルヌーイの定理は、
$$\frac{v_{2}^{2}-v_{1}^{2}}{2}+g(z_{2}-z_{1})+\frac{P_{2}-P_{1}}{ρ}=0・・・(1)$$
(1)式で表されます。
第一項が運動エネルギー、第二項が位置エネルギー、第三項が圧力を表わし、流体の持つエネルギーはこれらの項の総和となります。
なおかつ、運動エネルギーや圧力が位置エネルギーに変換可能であることを意味しています。
これは工業的に非常に重要な意味合いを持ちます。
なぜなら、ポンプで圧力をかければ流体を高いところまで持ち上げられることを示しているからです。
プラントは立地に制約があるため、ストラクチャーを組んで縦に長い構造物になることがよくあります。
熱交換器や蒸留塔、撹拌槽等の装置はストラクチャー内の高い位置に設置されることもあるため、そこまで流体を運ぶ必要があります。
このベルヌーイの定理が成り立つおかげで、エンジニアは流体を所定の高さまで持ち上げるのにどのくらいのエネルギーやポンプ揚程が必要か計算できるわけです。
ベルヌーイの定理の導出
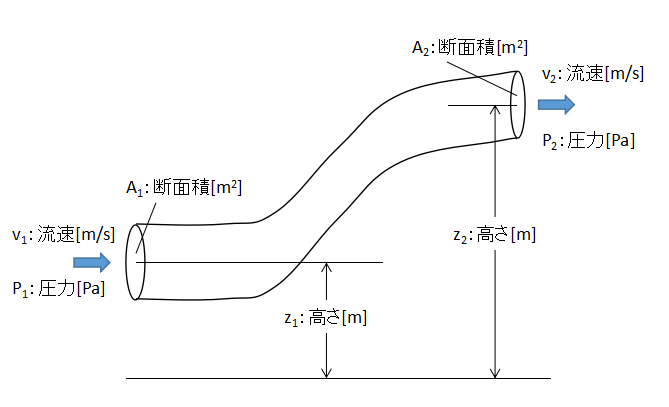
上図に示すような流管内の流動のエネルギー収支を取ります。
流体が完全流体だと仮定すると、流れに伴うエネルギー損失は無視できます。
ここで、流管入口出口における各エネルギー(運動エネルギー、位置エネルギー、圧力)について考えます。
高校で習う剛体の物理学では各エネルギーは
$$運動エネルギー=\frac{1}{2}mv^{2}・・・(2)$$
$$位置エネルギー=mgz・・・(3)$$
$$圧力による仕事(力×距離)=PA・x・・・(4)$$
m:物質の質量[kg]、v:物質の速度[m/s]、g:重力加速度[m/s2]
z:物質の位置[m]、P:圧力[Pa]、A:力の働く面積[m2]、x:移動距離[m]
(2)~(4)式となります。
各式の単位はそれぞれkg・m2/s2=N・m=J(ジュール)となり、エネルギーの単位となっていることがわかります。
基本的には(2)~(4)式を流体について当てはめて、入口出口でエネルギー収支を取るとベルヌーイの定理の形となります。
まず流体の質量は、流体密度ρ[kg/m3]、体積流量F[m3/s]、流体の流れる時間dt[s]で
$$ρFdt$$
上のように表されます。
体積流量Fはその区間の断面積A[m2]と流速v[m/s]で
$$F=Av$$
と表すことができます。
また、流体の移動距離x[m]は流速v[m/s]と流体の流れる時間dt[s]で
$$x=vdt$$
となります。
以上の関係より、流管入口のエネルギーと出口のエネルギーが保存され等しいとすると、

$$\begin{align}&\frac{1}{2}ρF_{1}dtv_{1}^{2}+ρF_{1}dt・g・z_{1}+P_{1}A_{1}・v_{1}dt\\&=\frac{1}{2}ρF_{2}dtv_{2}^{2}+ρF_{2}dt・g・z_{2}+P_{2}A_{2}・v_{2}dt・・・(5)\end{align}$$
(5)式となります。
左辺が流管入口のエネルギー、右辺が流管出口のエネルギーを示しています。
ここで、流体は常に連続的に流れているとすると、体積流量Fはどの場所でも等しいため、
$$F_{1}=F_{2}=v_{1}A_{1}=v_{2}A_{2}・・・(6)$$
(6)式となります。
(6)式で(5)式中の体積流量Fをv1A1に変換して、(5)式の両辺をρv1A1dtで割ると、
$$\begin{align}&\frac{1}{2}v_{1}^{2}+gz_{1}+\frac{P_{1}}{ρ}\\&=\frac{1}{2}v_{2}^{2}+gz_{2}+\frac{P_{2}}{ρ}・・・(7)\end{align}$$
(7)式となり、右辺-左辺=0の形にすると冒頭の(1)式となり、ベルヌーイの定理が導出できました。
$$\frac{v_{2}^{2}-v_{1}^{2}}{2}+g(z_{2}-z_{1})+\frac{P_{2}-P_{1}}{ρ}=0・・・(1)$$
ちなみに(7)式の両辺を重力加速度gで割ると、式の単位系がm(メートル)になります。
$$\frac{v_{1}^{2}}{2g}+z_{1}+\frac{P_{1}}{ρg}=\frac{v_{2}^{2}}{2g}+z_{2}+\frac{P_{2}}{ρg}$$
このとき、全エネルギー水頭H[m]は(8)式で表されます。
$$H=\frac{v^{2}}{2g}+z+\frac{P}{ρg}=一定・・・(8)$$
(8)式はポンプの揚程計算をするときにベースとなる式です。
式中の項はそれぞれ、
$$速度水頭:\frac{v^{2}}{2g}$$
$$位置水頭:z$$
$$圧力水頭:\frac{P}{ρg}$$
上のように呼ばれています。
現実の粘性流体への拡張
(1)式や(8)式は完全流体という粘性が働かない流体について成り立ちます。
しかし、現実の流体は粘性が働くため、摩擦等によるエネルギー損失が発生します。
そこで、(8)式を現実の流体に適用させるために、エネルギー損失を表わす項を(8)式に2つ追加します。
$$H=\frac{v^{2}}{2g}+z+\frac{P}{ρg}+h_{f}+h_{l}・・・(9)$$
(9)式がポンプの揚程を計算するときに使用される式です。
hfは摩擦損失水頭と呼ばれ、配管壁面での摩擦によるエネルギー損失を表わしています。
hlは形状損失水頭と呼ばれ、管路の急拡大・急縮小や曲がり部等の流路が大きく変化する箇所で生じるエネルギー損失を表わしています。
したがって、ポンプの揚程を計算するときは(9)式に従って、エネルギー損失分を上乗せして揚程を決定する必要があります。
