概要
粒子が大きくなると、流体中の粒子は慣性の効果により流体と同じ動きができなくなります。
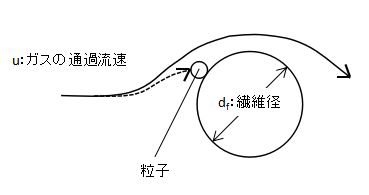
粒子を含む流体中にフィルター等の障害物を設置すると、流体は障害物を避けて流れますが、粒子は障害物を避けきれずに衝突し捕集されます。
このような慣性力を利用した捕集機構を慣性捕集機構といいます。
慣性捕集は数ある捕集機構の中でも主要なものの1つです。
流体の条件にもよりますが、10μm以上の大きさの粒子であれば慣性捕集で十分に除去することが可能です。
集塵機構
慣性効果による粒子の捕集は、基本的に粒子の運動方程式を解くことで求められます。
粒子レイノルズ数Rep≦2のストークス則が成り立つ領域では、
$$F_{d}=3πμd_{p}(u-v)・・・(1)$$
Fd:流体の抵抗力[N]、μ:流体粘度[Pa・s]、dp:粒子径[m]
u:流体速度[m/s]、v:粒子速度[m/s]
(1)式が成立します。(u-v)は粒子の相対速度を表わします。
粒子が大きくなるとストークス則で計算される抵抗力にずれが生じますから、通常はカニンガムの補正係数で(1)式を補正します。
$$F_{d}=\frac{3πμd_{p}(u-v)}{C_{c}}・・・(2)$$
Cc:カニンガムの補正係数[-]
(2)式を利用して、粒子の運動方程式を立てると、
$$m_{p}\frac{dv}{dt}=\frac{3πμd_{p}(u-v)}{C_{c}}+F_{e}・・・(3)$$
mp:粒子重量[kg]、Fe:粒子の受ける外力[N]
(3)式となります。
次に(3)式を(4)~(6)式を使用して無次元化します。
$$v_{n}=\frac{v}{u_{0}}・・・(4)$$
$$u_{n}=\frac{u}{u_{0}}・・・(5)$$
$$t_{n}=\frac{u_{0}t}{d_{f}}・・・(6)$$
vn:無次元粒子速度[-]、un:無次元流体速度[-]、tn:無次元時間[-]
u0:流れの平均速度[m/s]、d_{f}:繊維径[m]
また、粒子重量mpは、
$$m_{p}=ρ_{p}・\frac{4}{3}π(\frac{d_{p}}{2})^3=\frac{π}{6}ρ_{p}{d_{p}}^{3}・・・(7)$$
ρp:粒子密度[kg/m3]
(7)式で表されます。
(4)~(7)式を(3)式に代入すると、
$$\frac{π}{6}ρ_{p}{d_{p}}^{3}\frac{d(u_{0}v_{n})}{d(d_{f}t_{n}/u_{0})}=\frac{3πμd_{p}(u_{0}u_{n}-u_{0}v_{n})}{C_{c}}+F_{e}$$
$$\frac{C_{c}ρ_{p}{d_{p}}^{2}u_{0}}{18μd_{f}}\frac{dv_{n}}{dt_{n}}=(u_{n}-v_{n})+\frac{F_{e}}{u_{0}}\frac{C_{c}}{3πμd_{p}}$$
$$ψ\frac{dv_{n}}{dt_{n}}=(u_{n}-v_{n})+\frac{F_{e}}{u_{0}}\frac{C_{c}}{3πμd_{p}}・・・(8)$$
$$ψ=\frac{C_{c}ρ_{p}{d_{p}}^{2}u_{0}}{18μd_{f}}・・・(9)$$
ψ:慣性パラメーター[-]
(8)式となります。(8)式中のψは慣性パラメーターと呼ばれており、
$$Stk=2×ψ・・・(10)$$
慣性パラメーターの2倍がストークス数Stkとなります。
粒子の捕集効率は、理論的には(8)式の粒子の運動方程式を数値的に解くことで求められます。
ただし、(8)式を解くのは大変です。様々な推算式が発表されていますので、実用上は簡便な推算式を使用して捕集効率を求めることが多いでしょう。
捕集効率推算式
ここでは、慣性捕集効率ηI[-]のいくつか有名な推算式を紹介します。
Stechkinaらの式
$$η_{I}=\frac{Stk}{4{K_{u}}^{2}}(29.6-28α^{0.62})R^2-27.5R^{2.8}・・・(11)$$
$$K_{u}=-0.5{\rm{ln}}α+α-0.25α^2-0.75・・・(12)$$
$$R=\frac{d_{p}}{d_{f}}・・・(13)$$
$$Stk=\frac{C_{c}ρ_{p}{d_{p}}^{2}u_{0}}{9μd_{f}}・・・(14)$$
Ku:水力学因子[-]、α:フィルターの充填率[-]、R:さえぎりパラメーター[-]
Stechkinaらは慣性効果が比較的小さい領域で成り立つ式として、(11)式を発表しています。
0.0035<α<0.111、0.01<R<0.4が適用範囲とされています。
α=0.01、Rを3×10-5<R<3.0まで変化させたときのグラフを以下に示します。
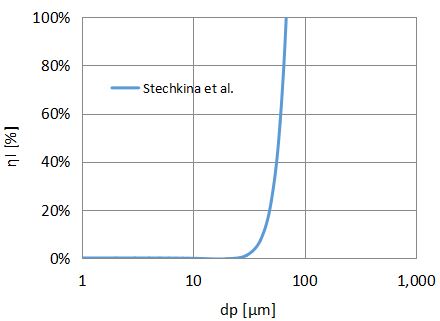
適用範囲外の領域で計算すると、慣性捕集効率ηIが負の値になったり、100%を超えたりするので気を付けましょう。
Landahl and Hermannの式
$$η_{I}=\frac{Stk^3}{Stk^3+1.54Stk^2+1.76}・・・(15)$$
$$Stk=\frac{C_{c}ρ_{p}{d_{p}}^{2}u_{0}}{9μd_{f}}・・・(16)$$
$$Re_{f}=\frac{ρd_{f}u}{μ}・・・(17)$$
LandahlとHermannは繊維レイノルズ数Ref=10で、(15)式を発表しています。
Ref=10のときのグラフを以下に示します。
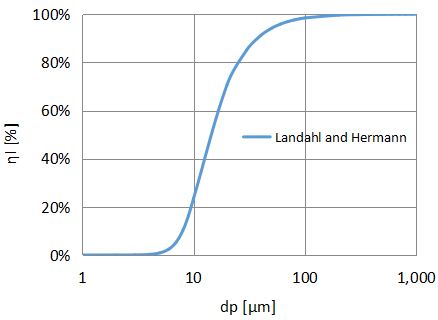
式の形として、ηIが0~100%の間に収まる点は良いですが、Ref≒10でどれほどの推算精度を保てるかはわかりません。
高橋の式
$$η_{I}={\rm{exp}}(-0.462α^{-0.5}Stk^{-1.0})・・・(18)$$
$$Stk=\frac{C_{c}ρ_{p}{d_{p}}^{2}u_{0}}{9μd_{f}}・・・(19)$$
α:フィルターの充填率[-]
高橋は0.005≦α≦0.1の範囲で慣性捕集効率ηIの線図をまとめており、定式化したものが(18)式です。
α=0.01、Ref=10のときのグラフを以下に示します。
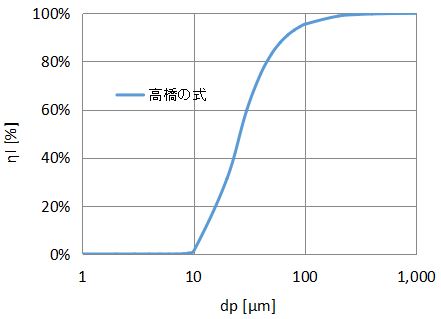
Landahl and Hermannの式と似たような値を示します。
まとめ
慣性捕集機構について解説しました。
この記事に示したもの以外にも推算式はたくさんあります。適用範囲をよく確認して使用するようにしましょう。
