概要
層流の配管流れにおける圧力損失と流速の関係式をハーゲン・ポアズイユの式といいます。
$$Δp=\frac{32μL\bar{u}}{d^{2}}・・・(1)$$
Δp:圧力損失[Pa]、μ:流体粘度[Pa・s]、L:配管長[m]
u:断面平均流速[m/s]、d:配管直径[m]
ハーゲン・ポアズイユの式は(1)式で表されます。
流体力学においては基礎的な式であり、大学の試験や資格などで出題されることが多いと思います。
本記事ではハーゲン・ポアズイユの式の導出について解説します。
ハーゲン・ポアズイユの式の導出
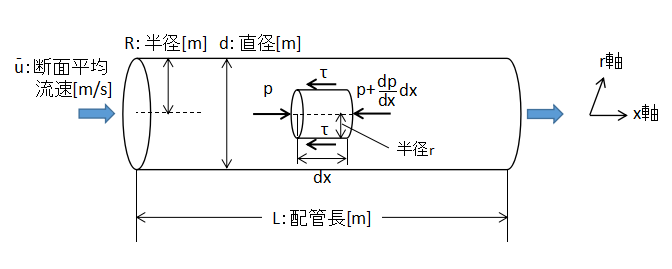
上図に示すような配管流れを考えます。
配管内の微小な円筒領域において力のつり合いで式を立てます。
$$流入面に作用する圧力=p・πr^{2}$$
$$流出面に作用する圧力=(p+\frac{dp}{dx}dx)・πr^{2}$$
$$円筒側面に作用するせん断応力=τ・2πrdx$$
これら3つの力は発達した流れにおいてつり合っているので、
$$p・πr^{2}-(p+\frac{dp}{dx}dx)・πr^{2}-τ・2πrdx=0・・・(2)$$
(2)式となります。
(2)式を整理すると、
$$τ=-\frac{dp}{dx}\frac{r}{2}・・・(3)$$
(3)式となります。
ここでニュートンの粘性法則から(4)式が成り立ちます。
$$τ=-μ\frac{du}{dr}・・・(4)$$
(3)式に(4)式を代入すると、
$$-\frac{dp}{dx}\frac{r}{2}=-μ\frac{du}{dr}$$
$$\frac{du}{dr}=\frac{dp}{dx}\frac{r}{2μ}・・・(5)$$
(5)式となります。
(5)式をr=Rからrまで積分します。r=Rのときは壁面なのでu=0、r=rのときはu=uとなりますから、
$$\int_{0}^{u}du=\int_{R}^{r}\frac{dp}{dx}\frac{r}{2μ}dr$$
$$u=-\frac{1}{4μ}\frac{dp}{dx}(R^{2}-r^{2})$$
$$u=\frac{R^{2}}{4μ}(-\frac{dp}{dx})(1-\frac{r^{2}}{R^{2}})・・・(6)$$
積分すると(6)式になります。
(6)式が層流の配管流れにおける流速分布を表わす式となります。
ちなみに最大流速umaxは配管中心となるため、(6)式においてr=0とすると
$$u_{max}=\frac{R^{2}}{4μ}(-\frac{dp}{dx})・・・(7)$$
(7)式で表されます。
続いて配管内を流れる流体の体積流量Qについて式を立てます。
体積流量は(6)式の任意の位置rにおける流速uを配管断面全体にわたって積分すれば算出できます。
$$\begin{align}Q&=\int_{0}^{R}u・2πrdr\\&
=\frac{πR^{2}}{2μ}(-\frac{dp}{dx})\int_{0}^{R}r(1-\frac{r^{2}}{R^{2}})dr\\&
=\frac{πR^{2}}{2μ}(-\frac{dp}{dx})[\frac{r^{2}}{2}-\frac{r^{4}}{4R^{2}}]^{R}_{0}\\&
=\frac{πR^{4}}{8μ}(-\frac{dp}{dx})・・・(8)\end{align}$$
積分すると(8)式となります。
(8)式で算出した体積流量Q[m3/s]を配管断面積で割れば断面平均流速を表わす(9)式が算出できます。
$$\bar{u}=\frac{Q}{πR^{2}}=\frac{R^{2}}{8μ}(-\frac{dp}{dx})・・・(9)$$
ちなみに(7)式の最大流速と(9)式を比較すると、
$$\bar{u}=\frac{1}{2}u_{max}・・・(10)$$
(10)式が成り立つことがわかります。
層流の配管流れで断面平均流速が最大流速の1/2になることは有名ですので覚えておきましょう。
次に(9)式の圧力勾配について、配管長Lの区間でΔpだけ圧力損失がかかるとすると、
$$-\frac{dp}{dx}=\frac{Δp}{L}・・・(11)$$
(11)式となります。
(11)式を(9)式に代入すると、
$$\bar{u}=\frac{R^{2}Δp}{8μL}$$
$$Δp=\frac{8μL\bar{u}}{R^{2}}$$
配管の半径Rを直径dに直すと(R=d/2)、
$$Δp=\frac{32μL\bar{u}}{d^{2}}・・・(1)$$
となり最初の(1)式を導出することができました。
おわりに
層流の配管流れで使用するハーゲン・ポアズイユの式を導出しました。
導出過程を理解しておけば、式を覚えることも簡単になります。一度は導出しておきましょう。
