概要
理想気体の状態変化は熱機関のサイクル等を考える上で非常に重要です。
熱機関は様々な状態変化を組み合わせてサイクルを作ることで仕事を取り出しています。
有名なサイクルをいくつか例に挙げると、
- カルノーサイクル(等温膨張⇒断熱膨張⇒等温圧縮⇒断熱圧縮)
- オットーサイクル(断熱膨張⇒定容冷却⇒断熱圧縮⇒定容加熱)
- ブレイトンサイクル(断熱膨張⇒定圧圧縮⇒断熱圧縮⇒定圧膨張)
などが挙げられます。
本記事では基本的な4つの状態変化である、定容変化、定圧変化、等温変化、断熱変化について解説します。
準静的過程
理想気体の状態変化を考えるうえで重要な前提が、準静的過程です。
ここでは例として、シリンダーとピストンからなる容器に封入した気体を定圧変化させることを考えます。
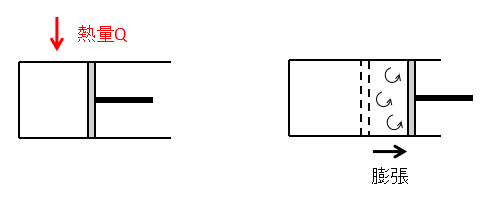
まず、状態1⇒状態2へ気体を膨張させます。
外部から気体に熱量Qを加えると気体の体積が増加するため、ピストンが右側に動きます。
このとき気体が急激に膨張すると、その過程で気体の渦流れなどが発生し乱れが生じます。
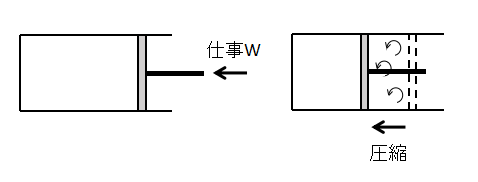
次に、状態2⇒状態1へと仕事Wをピストンに加えて気体を圧縮させます。
完全に状態1へ元に戻すためには、状態1⇒状態2への変化の過程で生じた気体の流れの乱れなども完全に逆向きに再現しなければなりません。
当然そのようなことは不可能であるため、状態2⇒状態1へ同じ経路を辿って戻すことはできず、実際のプロセスは全て不可逆過程となります。
しかし、理論的な取り扱いを考える上では可逆過程の方が簡単で都合がよいです。
そこで、シリンダー内の気体を常に熱平衡状態を保つようにものすごくゆっくりと変化させることで、状態1と状態2のどちらの方向にも移動させることが可能となります。
熱平衡状態とは、系のどの部分の温度・圧力も一定であることで、気体の流れの乱れなども発生しません。
このような、系の熱平衡状態を保ちながら無限にゆっくりと変化させる過程を準静的過程といいます。
熱力学の基礎理論では、特に注意書きがない限りは状態変化は可逆過程で考えます。
各状態変化
定容変化
気体の体積(容積)一定での状態変化です。
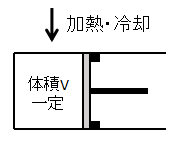
イメージとしては上図のようにピストンを固定した状態で気体を加熱・冷却するような変化となります。
P-V線図
ボイル・シャルルの法則において、V1=V2とすると、
$$\frac{P_{1}}{T_{1}}=\frac{P_{2}}{T_{2}}・・・(1)$$
P1,P2:状態1,2での圧力[Pa]、T1,T2:状態1,2での温度[K]
(1)式が成り立ちます。 また、P-V線図上で定容変化を表わすと下図のように直線となります。 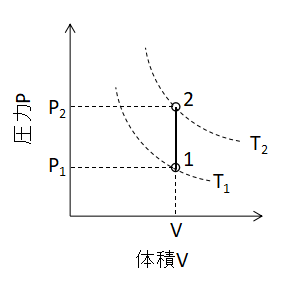
熱力学の第一法則から
体積Vが一定とみなせるためΔV=0となり、系が外にする仕事W12=0となります。 したがって、
$$Q_{12}=ΔU+W_{12}=ΔU・・・(2)$$
Q12:熱量[J]、ΔU:内部エネルギー変化[J]、W12:仕事[J]
(2)式となり、外部から加えられた熱量は全て内部エネルギーの増減に使用されます。
また、熱量Q12は定容比熱Cvを使用して、
$$Q_{12}=ΔU+W_{12}=mC_{v}(T_{2}-T_{1})・・・(3)$$
Cv:定容比熱[J/(kg・K)]
(3)式で表されます。
比エントロピー計算
定容変化の比エントロピー計算式は、
$$Δs=s_{2}-s_{1}=C_{v}{\rm{ln}}\frac{T_{2}}{T_{1}}・・・(4)$$
s1,s2:状態1,2での比エントロピー[J/(kg・K)]、T1,T2:状態1,2での温度[K]
Cv:定容比熱[J/(kg・K)]
(4)式で表されます。 また、T-S線図上で定容変化を表わすと下図のようになります。 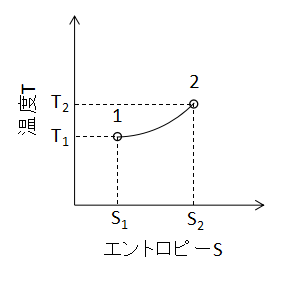
定圧変化
気体の圧力一定での状態変化です。
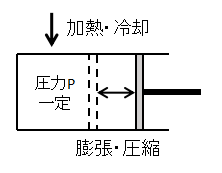
イメージとしては上図のように、気体に加えられた熱量によって気体が膨張・圧縮しピストンが動くような変化となります。
P-V線図
ボイル・シャルルの法則において、P1=P2とすると、
$$\frac{V_{1}}{T_{1}}=\frac{V_{2}}{T_{2}}・・・(5)$$
V1,V2:状態1,2での体積[m3]、T1,T2:状態1,2での温度[K]
(5)式が成り立ちます。 また、P-V線図上で定圧変化を表わすと下図のように直線となります。 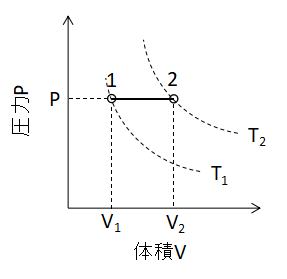
熱力学の第一法則から
圧力Pが一定とみなせるため、系が外にする仕事W12[J]は、
$$\begin{align}W_{12}&=\int_{V1}^{V2}PdV=P[V]^{V_{2}}_{V_{1}}\\& =P(V_{2}-V_{1})=PΔV・・・(6)\end{align}$$
(6)式のように簡単に積分して求めることができます。
したがって、熱量Q12は、
$$Q_{12}=ΔU+W_{12}=ΔU+PΔV・・・(7)$$
(7)式となります。
また、熱量Q12は定圧比熱Cpを使用して、
$$Q_{12}=mC_{p}(T_{2}-T_{1})・・・(8)$$
Cp:定圧比熱[J/(kg・K)]
(8)式で計算することができます。
比エントロピー計算
定圧変化の比エントロピー計算式は、
$$Δs=s_{2}-s_{1}=C_{p}{\rm{ln}}\frac{T_{2}}{T_{1}}・・・(9)$$
s1,s2:状態1,2での比エントロピー[J/(kg・K)]、T1,T2:状態1,2での温度[K]
Cp:定圧比熱[J/(kg・K)]
(9)式で表されます。 また、T-S線図上で定圧変化を表わすと下図のようになります。
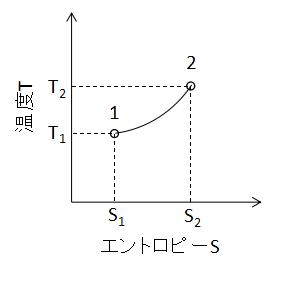
定容変化と定圧変化のT-S線図は見た目がほとんど同じであるため、変化の判別にはP-V線図等の別の情報が必要となるでしょう。
等温変化
気体の温度一定での状態変化です。
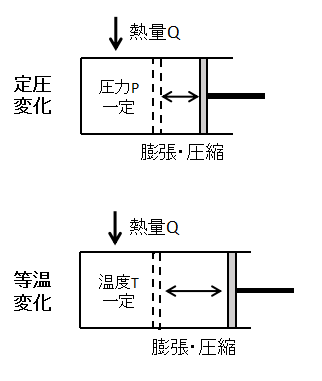
イメージとしては定圧変化と同様に気体が膨張・圧縮しピストンが動くような変化となります。
ただし、等温変化の場合、加えた熱量は全て仕事に変換されます。
したがって、定圧変化と同じ熱量を加えた場合は等温変化の方がピストンの動く距離が長くなります。
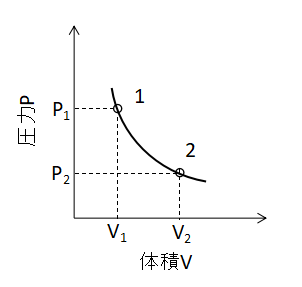
P-V線図
ボイル・シャルルの法則において、T1=T2とすると、
$$P_{1}V_{1}=P_{2}V_{2}・・・(10)$$
(10)式が成り立ちます。 また、P-V線図上で等温変化を表わすと下図のような曲線となります。
熱力学の第一法則から
系が外にする仕事Wは、
$$W_{12}=\int_{V1}^{V2}PdV=\int_{V1}^{V2}\frac{mRT}{V}dV・・・(11)$$
m:気体の質量[kg]、R:気体定数[kJ/(kg・K)]
(11)式で表されます。 ここで、等温変化では温度Tが圧力P、体積Vに依存せず一定とみなせるため、(11)式を積分することができます。
$$\begin{align}W_{12}&=mRT[{\rm{ln}}V]^{V_{2}}_{V_{1}}\\& =mRT{\rm{ln}}(\frac{V_{2}}{V_{1}})=mRT{\rm{ln}}(\frac{P_{1}}{P_{2}})・・・(12)\end{align}$$
積分すると(12)式となります。 また温度一定であるため内部エネルギー変化ΔU=0となることから熱量Q12は、
$$Q_{12}=ΔU+W_{12}=W_{12}・・・(13)$$
(13)式となります。
(13)式から、等温変化では加えた熱量が全て仕事に変換されることがわかります。
比エントロピー計算
等温変化の比エントロピー計算式は、
$$Δs=s_{2}-s_{1}=R{\rm{ln}}\frac{V_{2}}{V_{1}}・・・(14)$$
(14)式で表されます。 加えて、エントロピーの定義式から、
$$Δs=s_{2}-s_{1}=\frac{Q_{12}}{T}・・・(15)$$
(15)式と表すこともできます。 また、T-S線図上で等温変化を表わすと下図のようになります。 
断熱変化
気体と外部との間で熱のやり取りがない(Q=0)状態変化です。
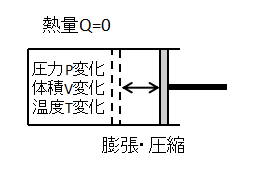
気体が断熱膨張して外部に仕事をすると、気体の体積Vは増加しますが気体の温度Tと圧力Pは減少します。
逆に気体が断熱圧縮して外部から仕事をされると、気体の体積Vは減少し気体の温度Tと圧力Pは増加します。
P-V線図
断熱変化をP-V線図で表すと下図のようになります。
 1→2への変化前後でP、V、T全てが変化するため、P-V線図においてはあまり特徴的ではありません。
1→2への変化前後でP、V、T全てが変化するため、P-V線図においてはあまり特徴的ではありません。
熱力学の第一法則から
断熱変化の場合は、次のポアソンの式である(16)、(17)式が成り立ちます。
$$P_{1}V_{1}^{γ}=P_{2}V_{2}^{γ}・・・(16)$$
$$T_{1}V_{1}^{γ-1}=T_{2}V_{2}^{γ-1}・・・(17)$$
γ:比熱容量の比[-]
断熱変化における仕事Wは(16)式を使用して導出します。(16)式から
$$PV^{γ}=P_{1}V_{1}^{γ}$$
$$P=P_{1}(\frac{V_{1}}{V})^{γ}$$
と変形して仕事の定義式に代入します。
$$\begin{align}W_{12}&=\int_{V1}^{V2}P_{1}(\frac{V_{1}}{V})^{γ}dV =P_{1}V_{1}^{γ}[-\frac{1}{γ-1}V^{-(γ-1)}]^{V_{2}}_{V_{1}}\\& =\frac{P_{1}V_{1}^{γ}}{γ-1}(V_{1}^{-(γ-1)}-V_{2}^{-(γ-1)})=\frac{P_{1}V_{1}}{γ-1}\Biggl(\frac{V_{1}^{-(γ-1)}}{V_{1}^{-(γ-1)}}-\frac{V_{2}^{-(γ-1)}}{V_{1}^{-(γ-1)}}\Biggr)\\& =\frac{P_{1}V_{1}}{γ-1}\Bigl(1-(\frac{V_{1}}{V_{2}})^{γ-1}\Bigr)=\frac{P_{1}V_{1}}{γ-1}\Bigl(1-(\frac{P_{2}}{P_{1}})^{\frac{γ-1}{γ}}\Bigr)・・・(17)\end{align}$$
最終的に(18)式の形となります。
また、断熱変化であるためQ=0となり、
$$ΔU=-W_{12}・・・(18)$$
(18)式が成り立ちます。
比エントロピー計算
等圧変化の比エントロピー計算式は、Q12=0であるためエントロピーの定義式(15)式から、
$$Δs=\frac{Q_{12}}{T}=0・・・(19)$$
(19)式となります。 また、T-S線図上で断熱変化を表わすと下図のようになります。 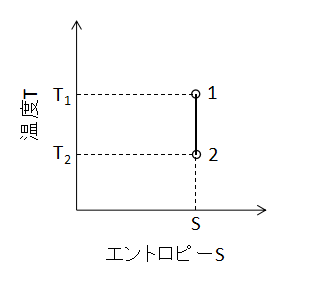
おわりに
理想気体の状態変化について解説しました。
定容変化、定圧変化、等温変化、断熱変化は熱機関の基礎ですので、覚えておきましょう。
