Outline
The overall heat transfer coefficient is used to determine the heat duty.
$$U=UAΔT・・・(1)$$
The equation to find the heat duty is Eq. (1).
where Q is the heat duty, U is the overall heat transfer coefficient, A is the heat transfer area, ΔT is the temperature difference.
The overall heat transfer coefficient is a parameter that depends on the fluid velocity, material, etc., and is given by
$$U=\frac{1}{\frac{1}{h_{o}}+r_{o}+\frac{x_{l}}{k}+r_{i}+\frac{1}{h_{i}}}・・・(2)$$
where ho is the outer heat transfer coefficient, ro is the outer fouling factor, xl is the thickness of material, k is the thermal conductivity of heat transfer tube, ri is the inner fouling factor, hi is the inner heat transfer coefficient.
Derivation of overall heat transfer coefficient
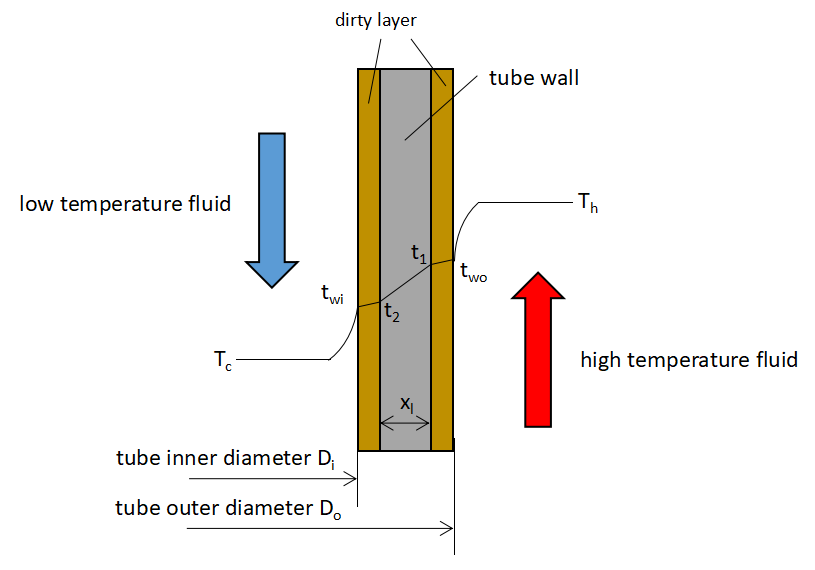
Consider the heat transfer around a heat transfer tube as shown in the above figure.
As an example, assume that a high-temperature fluid is flowing outside and a low-temperature fluid is flowing inside, and that the surface of the heat transfer tube is covered with a thin layer of dirt.
We will consider the heat transfer from the high temperature fluid to the low temperature fluid in this case.
In order not to have to think strictly about the length direction of the heat transfer tube, we will consider a section of small length dx of the heat transfer tube.
First, we consider the heat transfer from the hot fluid to the surface of the dirt layer.
Since Newton's cooling law of convective heat transfer holds,
$$dQ=h_{o}πD_{o}dx(T_{h}-t_{wo})・・・(3)$$
where dQ is the heat duty in a small section, Do is the the outer diameter of heat transfer tube, Th is the bulk temperature of high temperature fluid, two is the surface temperature of dirt adhering to the outer surface of the heat transfer tube.
πDodx means the heat transfer area.
Next, we consider the dirty layer on the outer surface of the heat transfer tube.
In the dirty layer, the inverse of the dirty coefficient r is the heat transfer coefficient, and the heat transfer to the outer surface of the heat transfer tube is given by
$$dQ=\frac{1}{r_{o}}πD_{o}dx(t_{wo}-t_{1})・・・(4)$$
where ro is the fouling factor of outer surface of heat transfer tube, t1 is the outer surface temperature of heat transfer tube.
Since the thickness of the dirty layer is very thin, the diameter of the dirty layer is considered to be the outer diameter of the heat transfer tube Do.
Next, we consider the heat transfer from the outer surface of the heat transfer tube to the inner surface.
Since the Fourier's law of conduction heat transfer holds for the inside of the heat transfer tube
$$dQ=\frac{k}{x_{l}}πD_{m}dx(t_{1}-t_{2})・・・(5)$$
where Dm is the mean diameter of heat transfer tube, t2 is the Inner surface temperature of heat transfer tube.
The average diameter of the heat transfer tube Dm is given by
$$D_{m}=\frac{D_{o}-D_{i}}{ln(D_{o}/D_{i})}・・・(6)$$
Next, we consider the dirty layer on the inner surface of the heat transfer tube.
Since it can be considered as the same as the outer surface, the equation is given by
$$dQ=\frac{1}{r_{i}}πD_{i}dx(t_{2}-t_{wi})・・・(7)$$
where Di is the inner diameter ot heat transfer tube, twi is the surface temperature of the dirt adhering to the inner surface of the heat transfer tube.
Similarly, since the thickness of the dirt layer is thin, the diameter of the dirt layer is considered to be the inner diameter of the heat transfer tube Di.
Finally, we consider the heat transfer from the surface of the dirty layer to the low-temperature fluid.
Similarly, since Newton's cooling law for convective heat transfer holds
$$dQ=h_{i}πD_{i}dx(t_{wi}-T_{c})・・・(8)$$
where Tc is the bulk temperature of low temperature fluid.
The point is that the heat duty in each section is constant at dQ for all steady state conditions.
Next, Eq. (4)~(8) are transformed so that the right-hand side contains only the term for the temperature difference.
$$\frac{dQ}{h_{i}πD_{o}dx}=T_{h}-t_{wo}$$ $$\frac{dQ}{\frac{1}{r_{o}}πD_{o}dx}=t_{wo}-t_{1}$$ $$\frac{dQ}{\frac{k}{x_{l}}πD_{m}dx}=t_{1}-t_{2}$$ $$\frac{dQ}{\frac{1}{r_{i}}πD_{i}dx}=t_{2}-t_{wi}$$ $$\frac{dQ}{h_{i}πD_{i}dx}=t_{wi}-T_{c}$$
Transform the equation in this way and add the five equations together side by side.
Then two, t1, t2, and twi on the right side disappear cleanly.
$$dQ\frac{1}{h_{o}πD_{o}dx+\frac{1}{r_{o}}πD_{o}dx+\frac{k}{x_{l}}πD_{m}dx+\frac{1}{r_{i}}πD_{i}dx+h_{i}πD_{i}dx}=T_{h}-T_{c}・・・(9)$$
There are two ways to summarize the heat transfer tubes: based on the outer diameter or based on the inner diameter.
Either can be used, but we will use the outer diameter standard here.
If the area of the outer surface of the heat transfer tube is Ao, dAo is expressed by Eq. (10).
$$dA_{o}=πD_{o}dx・・・(10)$$
Transforming the left-hand side into the equation,
$$\frac{dQ}{πD_{o}dx}[\frac{1}{h_{o}}+r_{o}+\frac{x_{l}}{k}(\frac{D_{o}}{D_{m}})+r_{i}(\frac{D_{o}}{D_{i}})+\frac{1}{h_{i}}(\frac{D_{o}}{D_{i}})]=T_{h}-T_{c}$$
$$\frac{dQ}{dA_{o}}[\frac{1}{h_{o}}+r_{o}+\frac{x_{l}}{k}(\frac{D_{o}}{D_{m}})+r_{i}(\frac{D_{o}}{D_{i}})+\frac{1}{h_{i}}(\frac{D_{o}}{D_{i}})]=T_{h}-T_{c}$$
The term in [ ] is transferred to the right-hand side, and is called the overall heat transfer coefficient based on the outer diameter Uo.
$$U_{o}=\frac{1}{\frac{1}{h_{o}}+r_{o}+\frac{x_{l}}{k}(\frac{D_{o}}{D_{m}})+r_{i}(\frac{D_{o}}{D_{i}})+\frac{1}{h_{i}}(\frac{D_{o}}{D_{i}})}・・・(11)$$
In summary, we can derive Eq. (12).
$$dQ=U_{o}dA(T_{h}-T_{c})$$
$$Q=U_{o}AΔT・・・(12)$$
The overall heat transfer coefficient of the inside diameter standard Ui can be organized in the same way by using Eq. (13).
$$dA_{i}=πD_{i}dx・・・(13)$$
When the thickness of the heat transfer tube is thin and the outer and inner diameters are almost the same, the equation may be simplified to Do≈Di≈Dm.
$$U=\frac{1}{\frac{1}{h_{o}}+r_{o}+\frac{x_{l}}{k}+r_{i}+\frac{1}{h_{i}}}・・・(14)$$
Reference values for overall heat transfer coefficient
The overall heat transfer coefficient is an important index in the design of heat exchangers, and its value is empirically known depending on the fluid being handled.
| High temperature fluid | Low temperature fluid | Overall heat transfer coefficient U [W/(m2K)] |
Water Methanol Ammonia Aqueous solution | Water | 1400 - 2900 |
Organic fluid (viscosity less than 0.5 cp) | Water | 400 - 900 |
Organic fluid (viscosity 0.5 - 1.0 cp) | Water | 300 - 700 |
Organic fluid (viscosity more than 1.0 cp) | Water | 30 - 450 |
| Gas | Water | 10 - 300 |
| Water | Brine | 600 - 1150 |
Organic fluid (viscosity less than 0.5 cp) | Brine | 250 - 600 |
| Steam | Water Methanol Ammonia Aqueous solution (viscosity less than 2.0 cp) | 1150 - 4050 |
| Steam | Aqueous solution (viscosity more than 2.0 cp) | 600 - 2900 |
| Steam | Organic fluid (viscosity less than 0.5 cp) | 600 - 1150 |
| Steam | Organic fluid (viscosity 0.5 - 1.0 cp) | 300 - 600 |
| Steam | Organic fluid (viscosity more than 1.0 cp) | 35 - 350 |
| Steam | Gas | 30 - 300 |
Organic fluid (viscosity less than 0.5 cp) | Organic fluid (viscosity less than 0.5 cp) | 250 - 450 |
Organic fluid (viscosity 0.5 - 1.0 cp) | Organic fluid (viscosity 0.5 - 1.0 cp) | 100 - 350 |
Organic fluid (viscosity more than 1.0 cp) | Organic fluid (viscosity more than 1.0 cp) | 50 - 250 |
Organic fluid (viscosity more than 1.0 cp) | Organic fluid (viscosity less than 0.5 cp) | 150 - 350 |
Organic fluid (viscosity less than 0.5 cp) | Organic fluid (viscosity more than 1.0 cp) | 50 - 250 |
The above table shows the overall heat transfer coefficients for typical fluid combinations.
If you know the U-value as a rough guide, you can roughly check whether the value you calculated is correct.
This is useful for those times when there is an occasional shift of a digit or two due to a unit conversion error. However, if you deviate from the standard design specifications, you may not be able to rely on them.

