Outline
The mixing Reynolds number is a dimensionless number that applies the Reynolds number to mixing.
The mixing Reynolds number is expressed by Eq. (1).
$$Re=\frac{ρnd^{2}}{μ}・・・(1)$$
where ρ is the liquid density, n is the agitation speed, d is the impeller diameter, μ is the liquid viscosity.
Depending on the value of the mixing Reynolds number, it is possible to determine whether the flow is laminar, transitional, or turbulent.
As a rough guide, they can be categorized as follows.
Laminar flow:Re≦50
Transitional flow:50<Re<1000
Turbulent flow:1000≦Re
Industrially, it is preferable to design in a turbulent flow with good mixing.
Laminar flow tends to cause stagnation of flow in the system, which leads to concentration and temperature distribution.
Contamination and corrosion of equipment also often occur in these stagnant areas.
Example of use of mixing Reynolds number
The mixing Reynolds number is often used in combination with other dimensionless numbers.
Here are some examples.
Calculation of power number Np
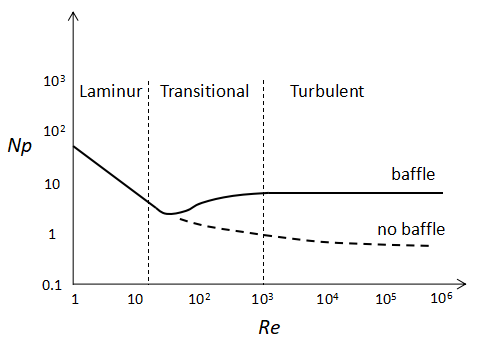
A graph with the power number Np on the vertical axis and the mixing Re on the horizontal axis is shown above.
The commonly known mixing impellers will have this characteristic curve. This curve is called the Np-Re curve.
In a laminar basin where the mixing Re is small, Np is inversely proportional to the mixing Re.
In a turbulent basin with large mixing Re, the value of Np varies depending on the presence or absence of baffles.
If there is a baffle, the value of Np is a constant value in the turbulent basin.
When there is no baffle, Np tends to decrease little by little as the mixing Re increases.
In practice, we calculate the mixing Re and read the power number Np from the graph of the Np-Re curve, or if this curve is formulated, we substitute the value of the mixing Re into the equation to obtain Np.
Calculation of the Nusselt number Nu
In order to know the heat transfer capacity of the stirred tank, it is necessary to calculate the boundary film heat transfer coefficient h and the Nusselt number Nu.
In heat transfer calculations for heat exchangers, Nu is famously calculated from the correlation equation between Re and the Prandtl number Pr. Similarly in the stirred tank, Nu is expressed as a correlation equation between mixing Re and Pr.
$$Nu=CRe^{a}Pr^{b}(\frac{μ}{μ_{w}})^c$$
where μ is the viscosity of bulk fluid, μw is the liquid viscosity near the wall, a,b,c are the coefficient dependent on equipment and stirring conditions.
Nu is calculated from the mixing Re and Pr, and the boundary film heat transfer coefficient h is calculated from Nu.

